Let $a$, $b$, $c$,$d$, $e$, $f$ distinct complex number on the same circle. Then the chords $ab$, $cd$, $ef$ are concurrent ( possibly at infinity) if and only if $$ \det\left( \begin{matrix} 1&a+b&ab\\ 1&c+d&cd\\ 1&e+f&ef \end{matrix}\right)=0 $$
The condition is invariant under complex affine transformations, so one may assume $a$, $\ldots$, $f$ on the unit circle.
Note that if moreover $b=\bar a = \frac{1}{a}$ and so on, then the chords $ab$, $cd$, $ef$ are perpendicular to the $x$ axis, so parallel. Clearly the determinant is $0$ also.
Clarifies a bit the calculations showing that some chords of a regular $n$-gon ar concurrent.
Provided as reference. I know the answer to my question and will add it soon.
$\bf{Added:}$ Consider a regular $30$-gon like in the picture.
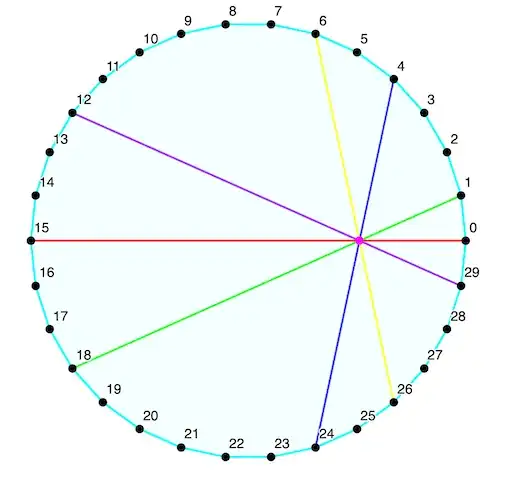
We have $5$ concurrent chords. We can check this by showing that the matrix
$$\left( \begin{matrix} 1&0&-1\\ 1&z+z^{18}&z^{19}\\ 1&z^4+z^{24}&z^{28}\\ 1&z^6+z^{26}&z^{32}\\ 1&z^{12}+z^{29}&z^{41} \end{matrix}\right)$$
has rank less then $3$, where $z$ is a primitive root of $1$ of order $30$. One checks that the vector $(1+z^{13}, -z-z^{12}, 1+z^{13})$ is in its kernel. Note the cyclotomic polynomial $\phi_{30}(z)= 1+z-z^3-z^4-z^5+z^7+z^8$.
$\bf{Added:}$ There is a similar formula in this post. This one seems easier to fathom, and also remember.
$\bf{Added:}$
A great for intersecting chords in regular $n$-gons is the paper by Bjorn Poonen and Michael Rubenstein ( kindly provided by @Gerry Myerson:)
The formula of @Jean Marie:, and why it is really equivalent: the rows of the determinant are $(\sqrt{a b}, \frac{1}{\sqrt{a b}}, \sqrt{\frac{a}{b}} + \sqrt{\frac{b}{a}})$, and one needs a factor of $\sqrt{a b}$ to get the one above.
Let's sketch the solution: the lines $ab$, $cd$, $ef$ are concurrent if and only the mixed product
$$\langle (1,a, \bar a)\times (1,b,\bar b), (1 c, \bar c)\times (1, d, \bar d), (1, e, \bar e)\times ( 1, f, \bar f) \rangle = 0$$
(basic linear algebra). Now if $|a|=\ldots = |f|=1$, then $$(1,a, \bar a)\times (1,b,\bar b)= (1, a, \frac{1}{a}) \times ( 1, b, \frac{1}{b})$$ and we get the result.