Question 1:
In Show that the map $s : X \longrightarrow \widetilde X$ is well-defined. the following condition was shown to be sufficient:
The normal lift of any loop in $X$ based at $x_0$ is a loop in $\tilde X$ based at $\tilde x_0$.
Let us call it the normal lift condition.
Theorem. The following are equivalent:
$s_u(x)$ independent of $u$.
The normal lift condition is satisfied.
$p_* : \pi_1(\tilde X, \tilde x_0) \to \pi_1(X, x_0)$ is an isomorphism.
$P(\tilde x_0)$ intersects $p^{-1}(x_0)$ only in $\tilde x_0$.
$P(\tilde x_0)$ intersects all $p^{-1}(x)$ only in a single point.
$P(\tilde x_0)$ is mapped by $p$ bijectively onto $X$.
Remark. Conditions 5. and 6. are much more transparent than the normal lifting condition. The proof that they are equivalent to 1. is almost trivial.
Proof of Theorem.
- $\implies$ 2. :
Let $u$ be a loop in $X$ based at $x_0$ and $\tilde u$ be its normal lift. Then $\tilde u (1) = s_u(1) = s_c(1) = \tilde x_0$, where $c$ is the constant loop based at $x_0$.
- $\implies$ 1. :
Let $u_i$, $i = 1,2$, be paths from $x_0$ to $x$ with normal lifts $\tilde u_i$. Then $w = u_1 * u_2^{-1}$ is a loop based at $x_0$. Its normal lift $\tilde w$ is a loop based at $\tilde x_0$, i.e. $\tilde w (1) = \tilde x_0$. Let $\tilde u_1$ be the normal lift of $u_1$ and $\tilde v$ be the lift of $u_2^{-1}$ starting at $\tilde u_1(1)$. Then $\tilde w = \tilde u_1 * \tilde v$, thus $\tilde v(1) = \tilde x_0$. Since $\tilde v^{-1}$ is the normal lift of $(u_2^{-1})^{-1} = u_2$, we get $s_{u_2}(x) = \tilde u_2(1) = \tilde v^{-1}(1) = \tilde v(0) = \tilde u_1(1) = s_{u_1}(x)$.
- $\implies$ 3. :
It is well-known that $p_*$ is always injective. Let $[u] \in \pi_1(X, x_0)$ and $\tilde u$ be its normal lift. It is a loop based at $\tilde x_0$, thus $[\tilde u] \in \pi_1(\tilde X, \tilde x_0)$. By construction $p_*([\tilde u]) = [p \circ \tilde u] = [u]$. This shows that $p_*$ is surjective.
- $\implies$ 2 :
Let $u$ be loop based at $x_0$. We have $p_*([v]) = [u]$ for some loop $v$ based at $\tilde x_0$. This means that the paths $u$ and $p \circ v$ are path homotopic (i.e. homotopic rel. $\{0,1\}$). Let $H : p \circ v \simeq u$ be a path homotopy. By homotopy lifting it has a lift $\tilde H$ such that $\tilde H(t,0) = v(t)$. The map $\tilde u (t) = \tilde H(t,1)$ is a lift of $u$. The maps $\phi_i(t) = \tilde H(i,t)$, $i = 0,1$, are lifts of the constant loop based at $x_0$. Since $\phi_i(I) \subset p^{-1}(x_0)$ and $p^{-1}(x_0)$ is discrete, the $\phi_i$ must be constant. Thus $\tilde u(i) = \tilde H(i,1) = \phi_i(1) = \phi_i(0) = H(i,0) = v(i) = \tilde x_0$, in particular $\tilde u$ is the normal lift of $u$. By construction it is a loop.
- $\implies$ 4. :
Let $\xi \in P(\tilde x_0) \cap p^{-1}(x_0)$. Choose a path $v$ from $\tilde x_0$ to $\xi$. Then $u = p \circ v$ is a loop based at $x_0$. But $v$ is the normal lift of $u$, thus it is a loop based at $\tilde x_0$. Hence $\xi = \tilde x_0$.
- $\implies$ 2. :
Let $u$ be a loop in $X$ based at $x_0$. Its normal lift $\tilde u$ starts at $\tilde x_0$ and ends a to some $\xi \in p^{-1}(x_0)$. Clearly $\xi \in P(\tilde x_0)$ which shows that $\xi \in P(\tilde x_0) \cap p^{-1}(x_0) = \{\tilde x_0 \}$. Thus $\tilde u$ is a loop in $\tilde X$ based at $\tilde x_0$.
- $\implies$ 5. :
Let $\xi_i \in P(\tilde x_0) \cap p^{-1}(x)$, $i = 1,2$, and let $v_i$ be paths in $\tilde X$ from $\tilde x_0$ to $\xi_i$. Then the $u_i = p \circ v_i$ are paths in $X$ from $x_0$ to $x$ and the $v_i$ are their normal lifts. Thus $\xi_i = s_{u_i}(x)$ which proves $\xi_1 = \xi_2$.
- $\implies$ 1. :
Let $u_i$ be paths in $X$ from $x_0$ to $x$, $i = 1,2$. Clearly $s_{u_i}(x) \in P(\tilde x_0) \cap p^{-1}(x)$, thus $s_{u_1}(x) = s_{u_2}(x)$.
- $\Longleftrightarrow$ 6 :
Trivial.
Question 2:
Let $p_0 : P(\tilde x_0) \to X$ be the bijection assured by the well-definedness of $s$. Then $s' : X \xrightarrow{s} P(\tilde x_0)$ is the inverse function of $p_0$. Therefore $s$ is continuous if and only if $p_0$ is a homeomorphism.
Theorem. If $\tilde X$ is path-connected, then $s$ is continuous.
Proof. In that case $p_0 = p$. But $p$ is an open map, thus $p_0$ is a homeomorphism.
Theorem. If $X$ is locally path-connected, then $s$ is continuous.
Proof. Let $V$ be an open neighborhood of $s(x)$ in $\tilde X$. There exists an evenly covered open neighborhood $U$ of $x$ in $X$ which means that $p^{-1}(U) = \bigcup_{\alpha \in A} V_\alpha$ with pairwise disjoint open $V_\alpha$ such that the restrictions $p_\alpha : V_\alpha \xrightarrow{p} U$ are homeomorphisms. We have $s(x) \in V_{\alpha(x)}$ for some $\alpha(x) \in A$. Thus $V \cap V_{\alpha(x)}$ is an open neighborhood of $s(x)$ in $\tilde X$. Hence $p(V \cap V_{\alpha(x)}) = p_{\alpha(x)}(V \cap V_{\alpha(x)}) \subset U$ is an open neighborhood of $x$ in $X$. Since $X$ is locally path-connected, $p(V \cap V_{\alpha(x)})$ contains a path-connected open neighborhood $U'$ of $x$ in $X$.
As a subset of $U$ also $U'$ is evenly covered with sheets $V'_\alpha = V_\alpha \cap p^{-1}(U') = p_\alpha^{-1}(U')$. The set $V'_{\alpha(x)} \subset V_{\alpha(x)} \subset V$ is a path-connected open neighborhood of $s(x)$ in $\tilde X$. Clearly $V'_{\alpha(x)}$ is contained in the path component of $s(x)$. Since $s(x) \in P(\tilde x_0)$, we get $V'_{\alpha(x)} \subset P(\tilde x_0)$. No other sheet $V_\alpha$ intersects $P(\tilde x_0)$. To see this, assume that there exists a point $\xi' \in V_\alpha \cap P(\tilde x_0)$. Let $\xi \in V_{\alpha(x)}$ be the unique point mapped by $p$ onto $x' = p(\xi') \in U'$. Then both $\xi, \xi'$ are contained in $p^{-1}(x') \cap P(\tilde x_0)$ which has only one element, thus $\xi \in V_{\alpha} \cap V_{\alpha(x)}$, a contradiction.
We conclude $p^{-1}(U') \cap P(\tilde x_0) = V_{\alpha(x)}$. Clearly $s(U') \subset p^{-1}(U) \cap P(\tilde x_0)$, i.e. $s(U') \subset V'$.
A shorter alternative proof is based on the fact that $\tilde X$ is locally path-connected because $p$ is local homeomorphism. Hence $P(\tilde x_0)$ is open (see here), thus $p_0$ is open since $p$ is is open. Hence $p_0$ is a homeomorphism. $\phantom{xxx} \square$
Let us give an example that $s$ is in general not continuous.
let $X$ be the Warsaw circle:
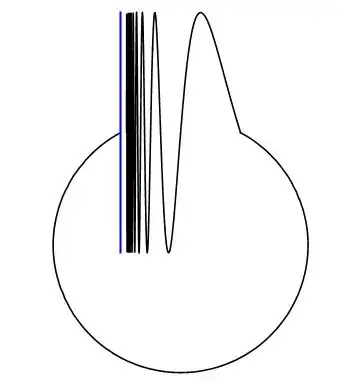
It has $n$-fold coverings $\tilde X$ obtained by pasting together $n$ copies of the closed topologist's sine curve $S$ into a "circular" pattern and $p$ mapping this space in the obvious way to $X$ by wrapping it $n$-times around $X$. This is in complete analogy to the coverings $z^n : S^1 \to S^1$. Drawing a picture is helpful.
Let $L \subset X$ be the line segment at which the $\sin(1/x)$-curve clusters and $C = X \setminus L$. Let $x_0 \in L$ the point where $C$ enters $L$ from the left. The space $\tilde X$ contains $n$ copies $L_i$ of $L$ and $C_i$ of $C$ in cyclic order $L_1, C_1, L_2, C_2, \ldots, L_n, C_n. L_1, C_1, \ldots$.
We let $\tilde x_0 \in L_n$ be the point such that $p(\tilde x_0) = x_0$. The path component $P(\tilde x_0)$ of $\tilde X$ containing $\tilde x_0$ is $C_{n-1} \cup L_n$ which is non-compact. $p$ maps it bijectively to $X$, thus the "normal lift construction" yields a function $s : X \to \tilde X$. But $p_0 : P(\tilde x_0) \to X$ is no homeomorphism, thus $s$ is not continuous. Actually it is not continous at $x_0$. Look at the picture to visualize this.
