4

Recently I've been studying Fourier analysis through Stein's book, and there is a section there dedicated to Weyl's Equidistribution Theorem, specifically,

A sequence $(\xi_n)_n$ in $[0, 1)$ is equidistributed if, and only if, for each $k\in\mathbb{Z}_{\neq 0}$ we have $$\lim_{N}\frac{1}{N}\sum_{n=1}^N e^{2\pi i k \xi_n}=0.$$

Now, I'm pretty confident that I understand Stein's proof, but I don't have any intuition for this result, and it uses a deep fact of Fourier analysis, that continuous functions can be approximated by trigonometric polynomials.

I think I got a nice intuition for the "only if" part: it is pretty straightforward to show (and intuitive to see) that if $(\xi_n)_n$ is equidistributed, so is $(\{k\xi_n\})_n$, and then for each $N$ the sequence $e^{2\pi i k \xi_1}, \dots, e^{2\pi i k \xi_N}$ behaves like the vertices of a $N$-sided regular polygon, and then its barycenter must be close to $0$, and the approximations get better as $N\to\infty$.

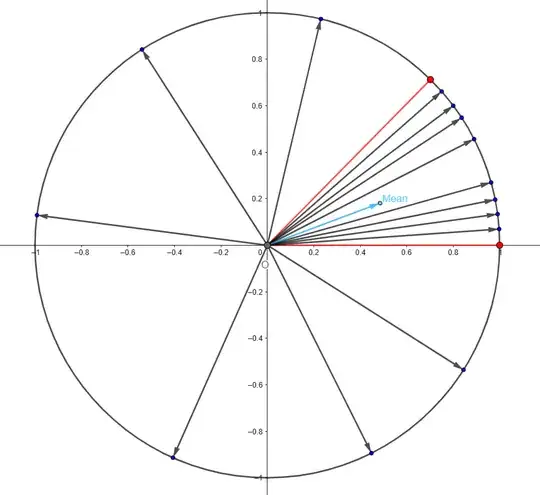
The "if" part is what I'm struggling with. I've tried the following. Suppose that $\xi_n$ is not equidistributed. Then there exists a interval $[a, b)$ and some $\varepsilon>0$ such that $$\left|\frac{\#\{1\le n\le N: \xi_n\in[a, b)\}}{N}-(b-a)\right|>\varepsilon$$ infinitely often. With some transformations, we can assume that $a=0$ (take $\xi_n'=\{\xi_n-a\}$). Moreover, we can assume that $$\frac{\#\{1\le n\le N: \xi_n\in[0, b)\}}{N}-b>\varepsilon$$ infinitely often (just take the interval [b, 1) otherwise and redo the previous step). Now, I hoped that there would be some $k$ such that, infinitely often, the points $e^{2\pi ik\xi_n}$ would cluster too much in some arc (because of the interval $[0, b)$), and this would prevent the mean from being too close from $0$. See the image below. But when I sat down to try to make sense of this argument, I couldn't get much further, as it is kinda hard to control the behavior of $\{k\xi_n\}$.

Does this idea have any truth to it, or is it a lost cause? Also, if you guys have other ideas, I'd like to read them.

I remind you thatt I'm just looking for some intuition, and the idea doesn't have to be super rigorous.

An example of my idea, if it worked as intended

SilverBladeII
  • 402
  • 1
    I thunk the ituitio comes from probability. Equidistribution of a sequence $\xi_n$ is "similar" drawing i.i.d samples $(U_n:n\in\mathbb{N})$ from the uniform distribution in $[0,1]$. The law of large numbers number will give you the "expected" result $\frac1n\sum^n_{k=1}e^{2\pi I k U_n}\xrightarrow{n\rightarrow\infty}0$ for $k\in\mathbb{Z}\setminus{0}$. – Mittens Jan 15 '24 at 15:46
  • you may want to hear directly from the Lion's mouth – Mittens Jan 15 '24 at 19:21
  • 1
    Typo: you presumably meant "for $k\not0$, rather than $k>0$... – paul garrett Jan 15 '24 at 21:15

2 Answers2

2

If you want to prove the "if" part by contraposition you could go on as follows. As you've noted there is some interval $[a,b)$ such that

$$\left|\frac{\#\{1\le n\le N: \xi_n\in[a, b)\}}{N}-(b-a)\right|>\varepsilon$$

for infinitely many $N$'s, which is equivalent with

$$\left\vert\frac{1}{N}\sum_{n\leq N}\mathbb{1}_{[a,b)}(\xi_n)-(b-a)\right\vert>\varepsilon$$ but then also $$\left\vert\frac{1}{N}\sum_{n\leq N}\sum_k c_k e(k\xi_n)-(b-a)\right\vert>\varepsilon/2$$ for infinitely many $N's$ where the inner sum a sufficiently good approximation of $\mathbb{1}_{[a,b)}$ so $$\left\vert\sum_k c_k \frac{1}{N}\sum_{n\leq N}e(k\xi_n)-(b-a)\right\vert>\varepsilon/2$$ for infinitely many $N$'s, hence there exists a $k_0$ s.t. $\lim_{N\to\infty}\frac{1}{N}\sum_{n\leq N}e(k_0\xi_n)\neq0$ (with $\neq0$ I mean that the limit doesn't exist or it exists and is not equal to zero) (note that the sum over $k$ is a finite sum).

1

Although it may be a little fancier than one might like, depending on tastes, the hypothesis is that the average (divide-by-$N$) of a sum (over $N$) of (periodic) Dirac deltas at the $\xi_k$ has Fourier series converging (weakly!) to $1$ (all other Fourier coefficients go to zero). This has seemed a "meaningful", as opposed to "technical", explanation of the hypothesis.

Even then, the conclusion is slightly delicate, since it is stronger than the "very weak" form of the hypothesis. :)

paul garrett
  • 55,317