How do I prove that in Mod(A), the following are equivalent: $P$ is projective; $0 \to M \to N \to P \to 0$ splits; and $P$ is stably free

Question

EDIT: I just discovered that this question has been asked before, my excuses. Here is the link: Every projective module is a direct summand of free module.

In my course in category theory, we have the following exercise. Prove that the following are equivalent in Mod(A):

1. $P$ is projective
2. $0 \to M \to N \to P \to 0$ splits
3. P is stably free

I worked out that 1 and 2 are equivalent using proposition 4.3.2. of Shapira's notes "Algebra and Topology" in the opposite category. 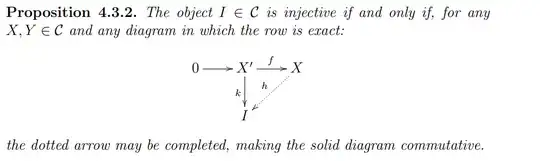From 3 to 1, I had the following, using again proposition 4.3.2 (reversing all the arrows, so $f: X \to X'$, $k: I \to X'$ and the diagram can be completed with $h: I \to X$.)

$P$ is stably free, so $A^{(I)} \simeq M \oplus P$ for an $M \in Mod(A)$. Assume that $k: P \to X'$ arbitrarily. Then, because $Hom_\mathcal{C}(\coprod_i X_i,Y) \simeq \prod_i Hom_\mathcal{C}(X_i, Y)$, and in an abelian category $\oplus \simeq \prod \simeq \coprod$, $k \oplus 0$ can be seen as a morphism from $M \oplus P \to X'$. Then there is an $h: M \oplus P \to X$, and this can be seen as $h_1 \oplus h_2$. Then $h_1$ is the map we are looking for to complete the diagram.

But I don’t know how to prove the last implication, so from 1 or 2 to 3.

Answer 1

For any module $P$ we can find a set $I$ and a surjection $g\colon A^{(I)}\twoheadrightarrow P$. We get a short exact sequence $0\to\mathrm{ker}(g)\to A^{(I)}\to P\to 0$, and because it splits, we find that $P$ is stably free.