1

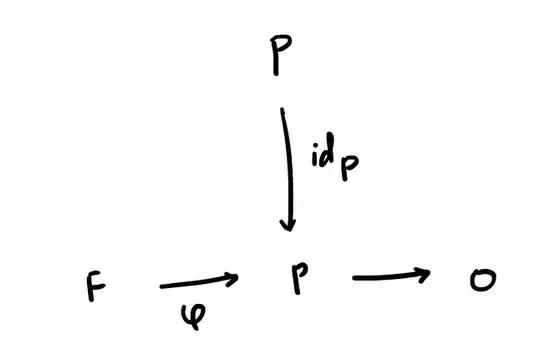
I was reading "Serial Rings" by Gennadi Puninski. There it is written that , "Since every module is a homomorphic image of a free module, every projective module is a direct summand of free module".(ie. if $P$ is a projective module, there exists a free module F such that, $ F=P \oplus T$ for some module $T$.)

But I can't understand how "Every module is a homomorphic image of a free module" implies that "Every projective module is a direct summand of free module".

(I have found a proof for "Every projective module is a direct summand of free module" but the first part of the above mentioned sentence wasn't used there.)

Potato
  • 83
  • 1
    The linked questions go very much into detail about every aspect of this problem. They seem to answer your question thoroughly, and with the same methods given in the answer you accepted here. – rschwieb Jun 24 '21 at 13:23

1 Answers1

1

Let $P$ be a projective module. We wish to show that it is the direct summand of a free module. Let $\varphi : F \to P$ be a surjection, where $F$ is a free module.

Consider the following diagram below.

enter image description here

Since $P$ is projective, there exists a map $\psi : P \to F$ making the following diagram commute.

enter image description here

It now follows that $F = \operatorname{im} \psi \oplus \ker \varphi$. But $\varphi \circ \psi = \operatorname{id}_P$ implies that $\psi$ is injective and thus, $\operatorname{im} \psi \cong P$, as desired.

Aryaman Maithani
  • 16,136
  • If someone can replace the images with code for the appropriate commutative diagrams, please feel free to do so. – Aryaman Maithani Jun 22 '21 at 11:00
  • Thank you very much sir. But can you prove it using the fact that, "Every module is a homomorphic image of a free module."? – Potato Jun 22 '21 at 11:09
  • 1
    @SuchandraKundu: I have used the fact when I said "Let $\varphi : F \to P$ be a surjection". Existence of such a $\varphi$ and $F$ is precisely the same as $P$ being the homomorphic image of a free module. – Aryaman Maithani Jun 22 '21 at 11:11
  • 1
    Okay thank you very much for clarifying. I am new to all these. – Potato Jun 22 '21 at 11:14