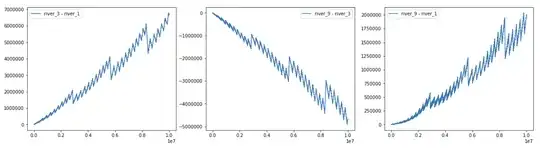
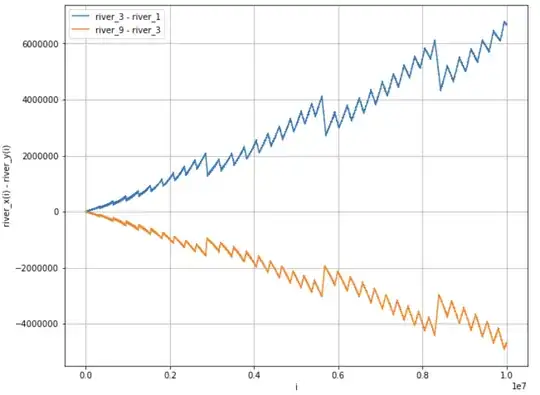
I came across this sequence called Digital River, where the next number in the sequence is defined as the sum of the digits of the previous number, plus, the previous number itself.
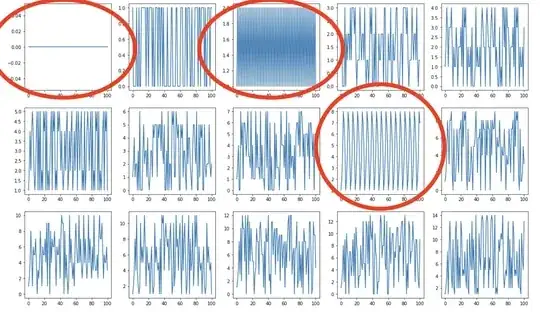
It caught my attention for some reason, and I wanted to analyse it. And I found some curious fractal-like patters. But let me begin by saying I am no mathematician, and I was just doing this recreationally, as I don't have the requisite tools and faculty to unwrap why these fractal-like patterns should appear. So I am posting my analysis notebook here in hopes of finding some answers.
Now, I have also come across the summatory Liouville function, and it too has similar fractal-like patterns. So, could it have something to do with, or is related in any way to, digital rivers? Some of the comments say that Liouville has something to do with the Riemann-Zeta function. Could the Riemann-Zeta function also explain why fractals appear in subtraction of digital rivers? If so, could you explain how, in a way that somebody without an undergrad degree in Math can understand the source of these fractal patterns?
And in doing so, could we formulate a theory or pattern of what other, similar kinds of sequences can show similar fractal-like patterns?
Here are some of the fractal-like patterns I've found, to pique your curiosity to download my notebook:
P.S. If this turns out to be an interesting problem that cannot be explained away trivially, and you want to work on analysing it together, then I'm happy to collaborate.