Explicit expression for simple roots of the root systems $A_2$, $B_2$ and $G_2$ in 2D

Question

I often find explicit expression for rank-2 root systems as $A_2$, $B_2$ and $G_2$ in a 3D Euclidean space. Does anybody have an explicit expression for the simple roots in terms of $e_1,e_2$ in the 2D Euclidean space $R^2$?

Answer 1

To get this off the unanswered list:

An explicit realization of a root system of type $A_n$ in $n$-dimensional Euclidean space (that is, with coroots / reflections defined to match the standard Euclidean inner product) is given in A description of the $A_n$-root system in terms of $\mathbb{R}^{n}$. For $n=2$ we can choose as basis

$$\alpha = \pmatrix{\sqrt2 \\0}, \beta = \pmatrix{-\sqrt{\frac12}\\ \sqrt{\frac32}}.$$

Of course if you are willing to rescale the product, you can use the easier realization

$$\alpha = \pmatrix{1 \\0}, \beta = \pmatrix{-\frac12\\ \frac12 \sqrt{3}}$$

by which you make them unit vectors. In any case this is the root system, and of course you can scale and rotate that to other coordinates as much as you want, as long as the relations between the roots stay rigid.

As for $B_2$, well, $B_n$ is usually given inside $\mathbb R^n$ as the set of $\pm e_i, \pm e_i \pm e_j$ (where the sign choices in the $\pm e_i \pm e_j$ are independent), so for $B_2$ you have as a basis e.g.

$$\alpha = \pmatrix{1 \\0}, \beta = \pmatrix{-1\\ 1}$$

and if you feel like it, you can list the other roots

$$\pmatrix{0 \\1}, \pmatrix{1\\ 1}, \pmatrix{-1 \\0}, \pmatrix{1\\ -1}, \pmatrix{0 \\-1}, \pmatrix{-1\\ -1}$$

You could have guessed that from the picture:

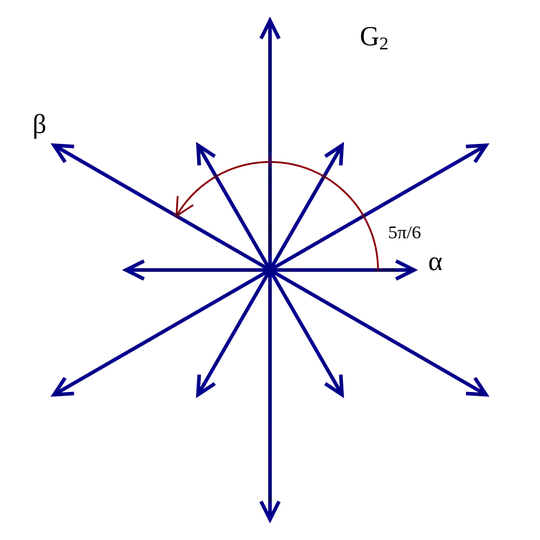
And as for $G_2$, well, this one again is more conveniently given in a plane in three-dimensional space, but nothing stops you from looking at

imagining a coordinate system behind it, declare $\alpha = \pmatrix{1 \\ 0}$ and, as an exercise, find the vector $\beta$ in the upper half-plane that has length $\sqrt3$ and such that its dot product with $\alpha$ gives $\cos(5\pi/6)$. From $\alpha$ and $\beta$ you get all other roots.

---

That all being said, I argue in the link above, as well as in answers to Picture of Root System of $\mathfrak{sl}_{3}(\mathbb{C})$, Canonical choice for simple roots?, and I don´t understand root systems, that such "explicit" realizations of root systems are of limited value.