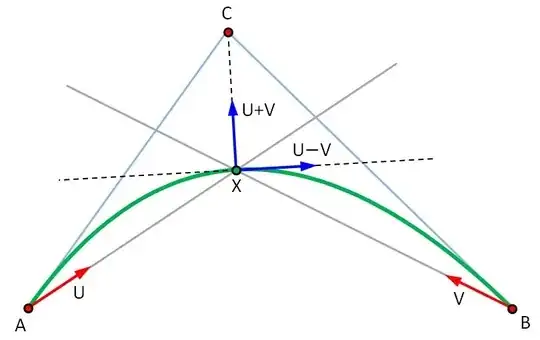
For simplicity of derivation, choose a coordinate system such that $\vec{X}$ is the origin.
The quadratic curve between $\vec{A}$ and $\vec{B}$ has the parametrization:
$$[0,1] \ni s \quad\mapsto\quad \vec{\gamma}(s) = (1-s)^2 \vec{A} + s^2 \vec{B} + 2s(1-s)\vec{C}$$
Since $\vec{X}$ lies on the quadratic curve, for some $t \in [0,1]$,
$\vec{\gamma}(t) = \vec{X} = \vec{0}$. This implies
$$\vec{C} = -\frac12 \left( \lambda^{-1} \vec{A} + \lambda \vec{B} \right)
\quad\text{ where }\quad \lambda = \frac{t}{1-t}.$$
So the problem of locating $\vec{C}$ reduces to the problem of figuring out the parametrization parameter $t$ for $\vec{X}$.
The tangent vector for the quadratic curve at $X$ is given by:
$$\gamma'(t) = \left.\frac{d\vec{\gamma}(s)}{ds}\right|_{s=t} = -2(1-t)\vec{A} + 2t\vec{B} + 2(1-2t)\vec{C} $$
Notice
$$\lambda = \frac{t}{1-t} \implies t = \frac{\lambda}{1+\lambda},\;\;1 - t = \frac{1}{1+\lambda} \;\;\text{ and }\;\; 1 - 2t = \frac{1-\lambda}{1+\lambda}$$
We find
$$ \gamma'(t) = -\frac{2}{1+\lambda}\vec{A} + \frac{2\lambda}{1+\lambda} \vec{B} - \frac{1 - \lambda}{1+\lambda}
\left( \lambda^{-1} \vec{A} + \lambda \vec{B} \right)
= \lambda \vec{B} - \lambda^{-1}\vec{A}
$$
The condition that $\vec{X}$ is the point on $\vec{\gamma}(s)$ closest to $\vec{C}$ can be expressed as:
$$\gamma'(t) \cdot \vec{C} = 0
\quad\iff\quad
\left( \lambda^2 \vec{B} - \vec{A} \right) \cdot \left( \lambda^2 \vec{B} + \vec{A} \right) =
\lambda^4 R_B^2 - R_A^2 = 0
$$
where $R_A = |\vec{A}| $ and $R_B = |\vec{B}|$.
This give us
$$\lambda = \sqrt{R_A/R_B}
\quad\implies\quad\vec{C} = -\frac{\sqrt{R_AR_B}}{2}\left( \frac{\vec{A}}{R_A} + \frac{\vec{B}}{R_B} \right)$$
Update
In the general case when $\vec{X}$ is not the origin, let
$$\vec{A} = (A_x,A_y),\;\;\vec{B} = (B_x,B_y),\;\;\vec{C} = (C_x,C_y),\quad\text{ and }\quad \vec{X} = (X_x,X_y).$$
The distances of $\vec{A}$, $\vec{B}$ from $\vec{X}$ become
$$\begin{cases}
R_A = & \sqrt{(A_x - X_x)^2 + (A_y - X_y)^2}\\
R_B = & \sqrt{(B_x-X_x)^2 + (B_y-X_y)^2},
\end{cases}$$
and the coordinates of $\vec{C}$ turns into:
$$\begin{cases}
C_x = & X_x -
\frac{\sqrt{R_A R_B}}{2}\left(\frac{A_x - X_x}{R_A} + \frac{B_x - X_x}{R_B}\right)\\
\\
C_y = & X_y -
\frac{\sqrt{R_A R_B}}{2}\left(\frac{A_y - X_y}{R_A} + \frac{B_y - X_y}{R_B}\right)
\end{cases}$$
- black curve is what we get, yellow is a desired curve. it looks nice only if you drag in the middle - that's why I was looking for a better solution
– bub
Sep 09 '13 at 23:53
