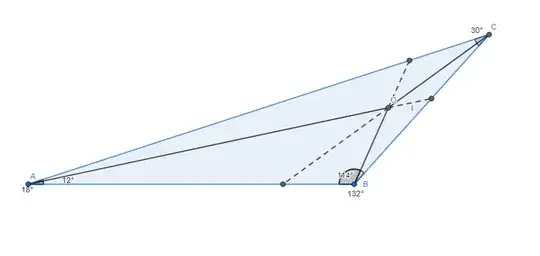
I provide another answer since the one given by sirious, despite being accepted, appears to be, so far, incomplete.
The idea orginates from the observation that the angles involved are related to those of regular pentagon and triangle.
We will therefore "carve out" triangle $ABC$ from the figure below, where $ABD$ is an isosceles triangle with $\measuredangle ADB = 108^\circ$, $BED$ is an equilateral triangle, and $BCE$ is an isoceles triangle with $\measuredangle EBC = 36^\circ$. See figure below.
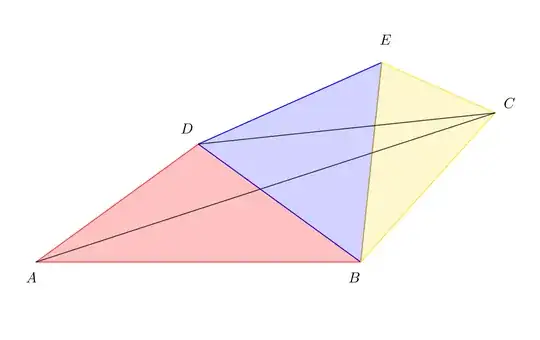
We first show that in fact $ABC$ is the triangle in OP. To this aim, note that $\measuredangle ABC = \measuredangle DEC = 132^\circ$, by angle chasing. Furthermore we have $BC:AB= EC:ED$ (side and diagonals respectively of regular pentagons. This is the key point in my proof, I believe.). Therefore $ABC \sim CED$ (SAS criterion). And since, by angle chasing, $\measuredangle EDC = 18^\circ$ and $\measuredangle ECD = 30^\circ$, we reach our conclusion.
Consider now the circle $(ABE)$, which is centered in $D$, and take on it point $O$ in such a way that $\measuredangle ODB = 24^\circ$.
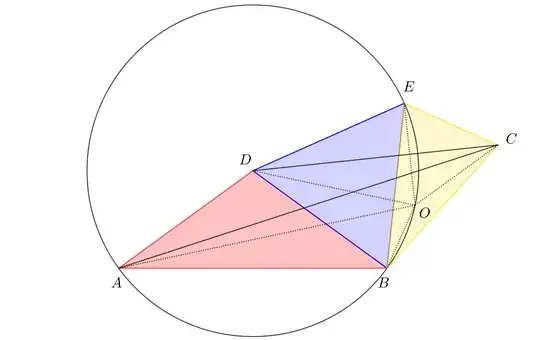
Let us verify that $O$ is the unique point that satisfies the hypotheses. We obviously have $\measuredangle OAB = \frac12 \measuredangle ODB= 12^\circ$, and $\measuredangle AOB = \frac12 \measuredangle ADB = 54^\circ$, therefore $\measuredangle ABO = 114^\circ$. We thus have $\measuredangle CBO = 18^\circ$, as in the hypotheses. Note that $BO$ bisects $\angle EBC$.
Our thesis is now reached, once we observe that $EBO \cong CBO$ (SAS criterion), and that $\measuredangle BEO = \measuredangle BAO = 12^\circ$. We conclude therefore that $$\boxed{\measuredangle BCO = 12^\circ}.$$