6

For which value of $k$ does the equation $x^4 - 4x^2 + x + k = 0 $ have four distinct real roots?

I found this question on a standardized test, and the answer presumably relies on a graphing calculator. Is there some method to solve this problem without the aid of a calculator?

Gamma Function
  • 5,752
T. Webster
  • 3,122
  • 1
    Simply find discriminant... (http://en.wikipedia.org/wiki/Discriminant). It must be positive. – Oleg567 Aug 24 '13 at 03:45
  • 1
    Notice that there is no cubic term: this tells us that the sum of the four roots is zero. The value of $ \ k \ $ is the product of these four roots. With the four roots being distinct, we must also have the sum of all six distinct products of pairs of the roots equal -4 (the quadratic coefficient) , and the sum of all four distinct products of three roots equal -1 (the negative of the linear coefficient). [BTW, was this a multiple-choice question? I ask because there is not a unique value for $ \ k \ $... ] – colormegone Aug 24 '13 at 03:59
  • Yes, the choices were 1, -2, 3. I don't quite follow what you said, though. I'll reread. – T. Webster Aug 24 '13 at 04:08
  • @Oleg567 it doesn't seem so easy to find the discriminant. This is a polynomial of the fourth degree. – Burt Jul 27 '21 at 03:35

3 Answers3

2

Discriminant of equation is $$ \Delta(k) = \begin{array}{|ccccccc|} 1 & 0 & -4 & 1 & k & 0 & 0 \\ 0 & 1 & 0 & -4 & 1 & k & 0 \\ 0 & 0 & 1 & 0 & -4 & 1 & k \\ 4 & 0 & -8 & 1 & 0 & 0 & 0 \\ 0 & 4 & 0 & -8 & 1 & 0 & 0 \\ 0 & 0 & 4 & 0 & -8 & 1 & 0 \\ 0 & 0 & 0 & 4 & 0 & -8 & 1 \end{array} = 256 k^3 - 2048 k^2 + 3520 k + 229. $$

If equation has distinct real roots, then discriminant is positive.

I hope we are talking about $k\in \mathbb{Z}$.

If $k\le -1$, then $\Delta(k)<0$.
$\Delta(0)=229>0$.
$\Delta(1)=1957>0$.
$\Delta(2)=1125>0$.
$\Delta(3)=-731<0$.
$\Delta(4)=-2075<0$.
$\Delta(5)=-1371<0$.
If $k\ge 6$, then $\Delta(k)>0$.

When $k\ge 6$, then $x^4 - 4x^2 + x + k>0$.

So, $k =0$, $k=1$, or $k=2$.

Links to see graphs/plots (and related info):
$x^4-4x^2+x+0$,
$x^4-4x^2+x+1$,
$x^4-4x^2+x+2$.

Oleg567
  • 17,740
  • I'm just a bit doubtful that this would be a method expected to be used for answering a standardized test question. It is also not something generally covered in "pre-calculus" courses. (Not that the approach I proposed is all that simple to implement, now that I've tried working with it. I'm still looking for something easier to calculate with...) – colormegone Aug 24 '13 at 04:44
  • @RecklessReckoner, it is just other method "without the aid of a (graphing) calculator". Tag "polynomials". – Oleg567 Aug 24 '13 at 04:50
  • Now that I re-read Trevor's original statement, I guess the use of graphers was permitted on the test (though that makes this not much of a problem...). I think another approach would be to determine the two values of $ \ k \ $ at which one of the "turning points" becomes a zero for the polynomial and find the choice that lies between those values, but that is also not covered in pre-calculus. – colormegone Aug 24 '13 at 04:56
  • @RecklessReckoner, maybe you are right. – Oleg567 Aug 24 '13 at 05:00
  • Thank you both for your answers. If it matters, I am going through this PRAXIS practice exam, question 5. – T. Webster Aug 24 '13 at 05:02
  • I think the choice of coefficients does not make for tidy results for the set of roots/zeroes in general (although setting $ \ k = 2 \ $ produces two integral zeroes and the other two are related to the "golden ratio"!). So while analytical methods to answer the question exist, they aren't "simple" for making calculations. – colormegone Aug 24 '13 at 05:07
  • @RecklessReckoner, yes, I think this method isn't appropriate for 2-hours testing... Graphing method is much faster/simpler here. – Oleg567 Aug 24 '13 at 05:12
1

Heck, I may as well just put this down as an "answer" (for which your question does not have just one)...

Notice that there is no cubic term: this tells us that the sum of the four roots is zero. The value of $ \ k \ $ is the product of these four roots. With the four roots being distinct, we must also have the sum of all six distinct products of pairs of the roots equal -4 (the quadratic coefficient) , and the sum of all four distinct products of three roots equal -1 (the negative of the linear coefficient). [BTW, was this a multiple-choice question? I ask because there is not a unique value for $ \ k \ $... ]

To clarify the above block of text a bit, consider your four roots to be $ \ p \ , \ q \ , \ r \ , \ \text{and} \ \ s \ $ . The factored form of the polynomial is then $ \ (x - p) \cdot (x - q) \cdot (x - r) \cdot (x - s) \ \ $ ; consider what happens once you multiply this out into a quartic polynomial. Among the choices you show, only $ \ k = 1 \ $ is correct.

colormegone
  • 11,002
  • +1 but I don't see why the absence of $x^3$ implies that the sum of the four roots is zero. Also, how do we know $k$ the product of these four roots? – T. Webster Aug 24 '13 at 04:11
  • A little better now? I thought I'd better write what I was describing a bit more mathematically... – colormegone Aug 24 '13 at 04:14
  • Better I guess, but I'm still having trouble seeing why we the sum of all six distinct products must equal $-4$...basically the entire second paragraph. Understanding that much is probably my responsibility, so I'll just mark as answered. – T. Webster Aug 24 '13 at 04:29
  • 1
    @Trevor These are Vieta's formulas for symmetric polynomials. See http://en.wikipedia.org/wiki/Vi%C3%A8te%27s_formulas – Cocopuffs Aug 24 '13 at 05:04
  • @RecklessReckoner I don't really understand this answer. Why is it obvious that $k=3$ isn't possible? – Cocopuffs Aug 24 '13 at 05:06
  • I don't think it's obvious by the approach I gave here, since the calculations aren't easy to resolve. That's why I used quotes around the word "answer" in my first sentence... – colormegone Aug 24 '13 at 05:47
  • @Cocopuffs Perhaps my other proposal for an answer is more useful for indicating the range $ \ k \ $ may have. My first idea is really too clumsy... – colormegone Aug 27 '13 at 02:10
  • 1
    @Trevor Urmm... what say we pass by this idea, which is a mess to work with (although it should be soluble theoretically, since it generates four non-linear equations in four unknowns) and consider the other answer I've posted... – colormegone Aug 27 '13 at 02:13
  • @Cocopuffs, thanks for the link to Vieta's Formulas. In which cases are Vieta's formulas generally useful to find the roots of polynomials? For example, how about this question – T. Webster Aug 28 '13 at 06:13
  • @Trevor This is a pretty deep question. The key word(s) is "Galois theory". Vieta's formulas are expressions for exactly the elementary symmetric polynomials in the roots, and you can find ANY symmetric expression in the roots this way. Unfortunately, in degree $5$ and higher, you can't use this to find the roots themselves - except in special cases – Cocopuffs Aug 28 '13 at 22:31
  • 1
    @Trevor For example, for a polynomial $f$ of degree $2$ with roots $r_1$ and $r_2$, we know $r_1 + r_2$ by Vieta's formula, and we can find $(r_1 - r_2)^2$, since this is symmetric in $r_1$ and $r_2$ - indeed $(r_1 - r_2)^2 = (r_1 + r_2)^2 - 4r_1 r_2$. This lets us find $r_1 - r_2$ (up to sign), and getting $r_1$ and $r_2$ is just linear algebra. In degree $3$ (Cardano's formula) you do the same, but considering $(r_1 + \zeta r_2 + \zeta^2 r_3)^3$ and $(r_1 + \zeta^2 r_2 + \zeta r_3)^3$, where $\zeta = e^{2\pi i/3}$ is the usual $3$-rd root of unity. – Cocopuffs Aug 28 '13 at 22:34
1

Here's another idea that may be easier to deal with (although the reasoning is a bit long for a standardized test question):

We start by noting that the polynomial $ \ f(x) \ = \ x^4 - 4x^2 + x + k \ $ has no symmetry about the $ \ y-$ axis. Since the leading coefficient is positive, the curve "opens upward". Some values of the polynomial function are

$$ f(-2) = k - 2 \ , \ f(-1) = k - 4 \ , \ f(0) = k \ , \ f(1) = k - 2 \ , \ f(2) = k + 2 \ , \ f(3) = k + 48 \ . \ $$

From this and the behavior of the "tails" of the curve, we can surmise that there are three "turning points" [I will avoid the language of calculus and not say "local extrema"].

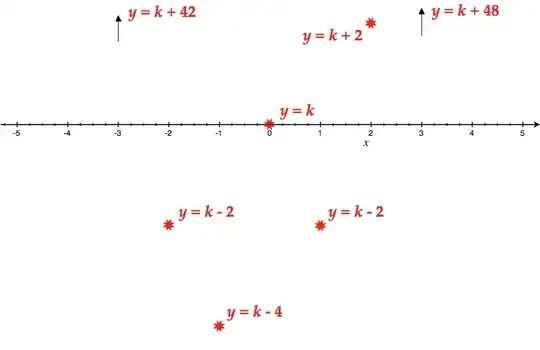
enter image description here

The relative positions of these points suggests the presence of "turning points" in the vicinity of $ \ x = -1 \ , \ x = 0 \ , \ \ \text{and} \ \ \ x = 1 \ . $

Taking $ \ k = 0 \ $ , the polynomial can be factored as $ \ x \ \cdot \ (x^3 - 4x + 1) \ $ . Descartes' "Law of Signs" tells us that the cubic polynomial has two or no positive real zeroes and one negative real zero. Together with the number of turning points and the lack of symmetry, we can conclude that there are four distinct real zeroes (one being $ \ x = 0 \ $). By the Intermediate Value Theorem (which is often mentioned, at least briefly in pre-calculus), the sign changes of the function indicate that the negative zero lies in $ \ x < -2 \ $ and the two positive zeroes are in the intervals $ \ 0 < x < 1 \ $ and $ \ 1 < x < 2 \ $ (the first of these really requires a little extra work, either by showing that there are positive values of the function in that interval, or by considering the form of the curve).

For $ \ k = -2 \ $ , all of the aforementioned function values are negative until we reach $ \ f(2) \ $ [in fact, $ \ x = 2 \ $ is a zero], so we are left with only two real zeroes in $ \ x < -2 \ $ and $ \ x > 2 \ $ .

For $ \ k = 3 \ $ , $ \ f(-2) = -1 \ $ and all the rest of the aforementioned function values are positive until we reach $ \ f(2) \ $ , so we lose the two positive real zeroes (the two real zeroes are in $ \ -2 < x < -1 \ $ and $ \ -1 < x < 0 \ $ ) .

[Upon consulting the graph, we find that the number of real zeroes will drop from four to two if the $ \ x-$axis lies "above" the turning point near $ \ x = 0 \ $ or "below" the one near $ \ x = 1 \ $ . This indicates that we must have $ \ \sim 0 \ < \ k \ < \ \sim 2 \ . $ ]

This leaves $ \ k = 1 \ $ -- upon checking the function values, we find the real roots are in the intervals $ \ x < -2 \ , \ -1 < x < -0 \ , \ 0 < x > 1 \ \ \text{and} \ \ 1 < x < 2 \ . $

This may still seem a little glib and call for a bit more calculating of function values, but does not actually require plotting a whole graph.

EDIT: added graph and elaborated on argument concerning permissible values of $ \ k \ $ .

colormegone
  • 11,002
  • I think this answer helps gain intuition on this type of problem. For the purpose of standardized tests, given 3-5 choices, it might be faster to guess and check. – T. Webster Aug 28 '13 at 05:16