2

This question is linked to a previous one that I asked:

Attempting to find a specific similarity (equivalence) matrix

I have a group of 24 elements, with two generators. I need to find an equivalence matrix $Q$ such that $A_i=Q^{-1}B_iQ$ where $B_i$ are permutation matrices and $A_i$ are block diagonal matrices, all with the same block diagonal form. The same $Q$ for all $A_i$ and $B_i$ needs to be found.

This is related to the symmetry group $O$ (rotations of a cube).

I read: http://www.mathworks.co.uk/matlabcentral/newsreader/view_thread/295993 and through suggested methods can find $Q$ for a specific pair $A_i,B_i$ but not a specific $Q$ that works for all pairs. I also find that each $Q$ is complex but it needs to be real.

I have a feeling that the form of the $Q$ that I'm looking for has no zeros and is fully populated with $1$ and $-1$, maybe multiplied by a constant, say $1/24$.

Help is much appreciated!

Edit: To clarify, for each element $g_1,...,g_{24}$ in my group $G$, I have a corresponding matrix representation $B_1,...,B_{24}$ with their corresponding block diagonal form $A_1,...,A_{24}$. I know all $A_i$ and $B_i$ (I have calculated these using the two generators).

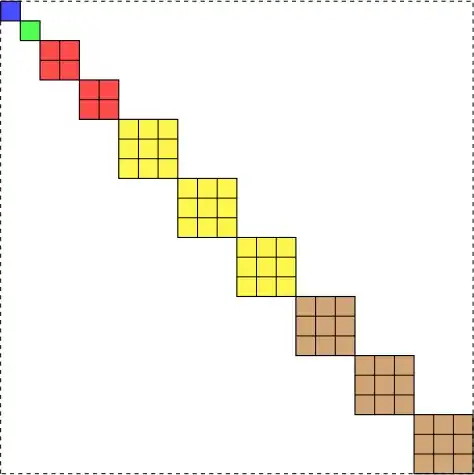
Edit 2: The block diagonal $A_i$ take the form shown in the image.

https://docs.google.com/file/d/0B6FgykLtWUXlbHRqOUd2XzNnbEU/edit?usp=sharing

The blocks with the same colour represent equivalent blocks (see comments from Marc below).

Community
  • 1
tiit_helimut
  • 153
  • What do the $A_i$ and $B_i$ have to do with the group? – Tobias Kildetoft Aug 22 '13 at 11:40
  • @TobiasKildetoft $B_i$ are the matrix representations of the elements in the group, $A_i$ are the corresponding representations but in block diagonal form. I know all of the $A_i$ and $B_i$ but am unsure of how to find the specific $Q$ that transforms all $B_i$ to the $A_i$. – tiit_helimut Aug 22 '13 at 11:43
  • It looks like you are trying to decompose a permutation representation of your group into irreducible(?) sub-representations. The blocks of the $A_i$ would specify your sub-representations. It would help to know more about those blocks, for instance do they indeed define irreducible representations? And if so, are they all different (inequivalent)? If both answers are affirmative, it will essentially suffice to find the isotypic components of your permutation representation. – Marc van Leeuwen Aug 22 '13 at 11:57
  • @MarcvanLeeuwen This is exactly what I'm doing. I'm aware that the set of $B_i$ are not unique but I have constructed a specific set. The $A_i$ do indeed decompose into irreducible representations. Each $A_i$ is different from every other $A_i$ but not every irreducible representation within each $A_i$ is different - is that what you are asking? – tiit_helimut Aug 22 '13 at 12:06
  • Comparing the $A_i$ among each other is not what I was asking about. The collection of all $A_i$ together form a representation. You say they all have the same block diagonal form, so those blocks define subrepresentations. The question is whether some of these blocks define equivalent representations (one block being similar to another block, with the same similarity being used for all $i$; this of course requires the blocks to be of the same size to begin with); if that happens it is a complication (hard to keep those blocks apart). If not, each gives a unique sub-repn of the $B_i$s repn. – Marc van Leeuwen Aug 22 '13 at 13:55
  • @MarcvanLeeuwen Yes - I see what you mean. It's hard to describe but yes there are equivalent "blocks": any block that is n×n (they are all square blocks) will be one of n equivalent blocks (if you see what I mean). I have added a link to an image in the main post (see edit 2). – tiit_helimut Aug 22 '13 at 16:28

0 Answers0