$\def\P{\operatorname P}$
The goal of the Fourier Legendre series is to find an exact explicit series solution to $x^x=x+1$, not just $x=a+b+c+\dots$ with unknown series coefficients. Lagrange reversion was attempted, but it failed to converge each time or the series coefficients were not able to be evaluated.
To find the Fourier Legendre $\P_n(x)$ series solution of $\frac{x^x}{x+1}=1$, we transform $\frac{x^x}{x+1}$ so it contains the points $(0,0)$ and $(1,1)$:
$$f(x)=\frac65\frac{(x+1)^{x+1}}{x+2}-\frac35$$ The solution of $\frac{x^x}{x+1}=1$ is the solution of $f(x-1)=\frac35$, so $x=1+f^{-1}\left(\frac35\right)\approx1.776775$. Now we find the Fourier Legendre expansion of $\begin{cases}f^{-1}(x)&0\le x\le 1\\0&-1\le x<0\end{cases}$ to avoid any singularities, shown below:
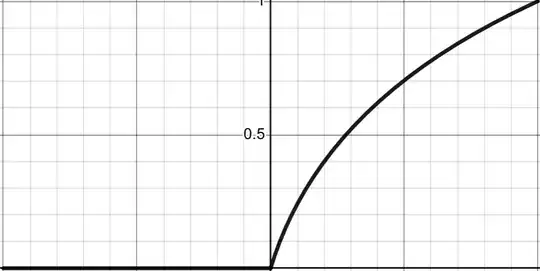
The Fourier Legendre series usually has integration bounds of $\int_{-1}^1$, but we have integration bounds of $\int_0^1$ as we graphed $y=0$ for $-1\le x<0$:
$$f^{-1}(x)=\sum_{n=0}^\infty \left(n+\frac12\right)\P_n(x)\int_0^1 \P_n(t) f^{-1}(t)dt= \sum_{n=0}^\infty \left(n+\frac12\right)\P_n(x) a_n$$
Substituting $t\to f^{-1}(t)$ gives a Stieltjes integral:
$$a_n=\int_0^1 t\P_n\left(\frac65\frac{(t+1)^{t+1}}{t+2}-\frac35\right)\ d\left(\frac65\frac{(t+1)^{t+1}}{t+2}-\frac35\right)$$
Now expand $\P_n\left(\frac65\frac{(x+1)^{x+1}}{x+2}-\frac35\right)=\P_n\left(z-\frac35\right)$ as a Taylor series at $z_0=-\frac35$ to have a polynomial in $\frac65\frac{(t+1)^{t+1}}{t+2}$ via Legendre $\P_n^k(x)$ expansion:
$$\P_n(z)=\sum_{k=0}^n\frac{(-1)^k \P_n^k(z_0)}{\left(1-z_0^2\right)^\frac2kk!}(z-z_0)^k$$
substitute $t\to t+1$ to get integration bounds of $\int_1^2$, and factor out the $\frac 65$ from $\frac 65\frac{t^t}{t+1}$:
$$a_n=\sum_{k=0}^n\frac{(-1)^k\P_n^k\left(-\frac35\right)}{\left(1-\left(-\frac35\right)^2\right)^\frac k2k!}\left(\frac 65\right)^{k+1}\color{blue}{\int_1^2(t-1)\left(\frac{t^t}{t+1}\right)^kd \left(\frac{t^t}{t+1}\right)}\tag1$$
integrating by parts:
$$\color{blue}{\int_1^2(t-1)\left(\frac{t^t}{t+1}\right)^kd \left(\frac{t^t}{t+1}\right)}=\frac{\left(\frac43\right)^{k+1}}{k+1}-\frac1{k+1}\int_1^2\left(\frac{t^t}{t+1}\right)^{k+1}dt\tag2$$
$\int_1^2\left(\frac{t^t}{t+1}\right)^{k+1}dt$ requires another series and special functions, but that is not our focus for now. The problem is that multiple softwares fail past about the $26$th partial sum
Wolfram Alpha
At $n=26$, Wolfram Alpha starts plotting the Fourier Legendre series at stage $(1)$ like so:
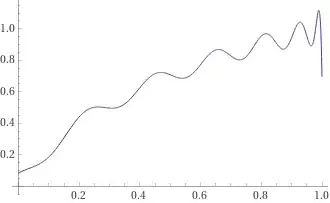
integration by parts in the series coefficients, from $(2)$, slightly reduces this effect:
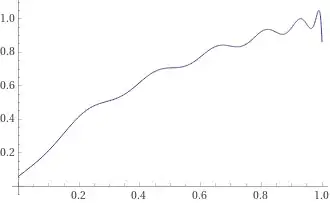
shown at $n=26$. However, plotting at $n=25$ of the same series gives a smooth curve as expected:
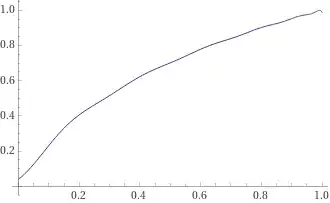
implying there is a calculation error starting around $n=26$. Maybe it is because $\int_0^1 \left(\frac{t^t}{t+1}\right)^{k+1}dt$, from $(2)$, grows into the ten thousands for $k\approx 26$ and the plotting discrepancy appears. Conversely, the series itself may diverge.
Mathematica (Wolfram Cloud)
This section uses the expansion from stage $(1)$. Unfortunately, past $n=10$ terms, computation time runs out:
and when $x=\frac35$, the Fourier Legendre series should give $x-1=0.776775\dots$, but it converges incorrectly past $n=26$ just like Wolfram Alpha:
$$\left[\begin{matrix}n&\text{partial sum}\\24&0.771697\\25&0.780971\\26&0.780639\\27&1.26721\\28&-0.648316\\30&6.7218\end{matrix}\right]$$
Typing in Sum[(n+1/2) LegendreP[n,3/5] NIntegrate[t LegendreP[n,(6/5 (t+1)^(t+1)/(t+2)-3/5)] D[6/5 (t+1)^(t+1)/(t+2),t],{t,0,1}],{n,0,25}] has convergence errors:
“Nintegrate: Nintegrate failed to converge to prescribed accuracy after 9 recursive bisections in t near {t} = <0.929672}. Nintegrate obtained 0.000539183 and 1.01235×10 integral and error estimates”
“Nintegrate: Numerical integration converging too slowly: suspect one of the following: singularity, value of the integration is 0, highly oscillatory integrand, or WorkingPrecision too small”
The gradual convergence for $0\le n\le 26$ is expected, but the issue for $n>26$ is not. The series seems to diverge due to software errors, but does it really diverge?

FindRoot[ x^x - x -1,{ x, 1.7}, WorkingPrecision->50]. Why Fourier-Legendre? – Somos Jun 24 '23 at 16:19