Is this proof of transitive property of implication correct?

Question

I would like to prove the transitive property of the implication symbol, namely:

Prove that assuming $(A \rightarrow B)$ and $(B \rightarrow C)$, it follows that $(A \rightarrow C)$.

I have attempted a proof below and would like to know if it is correct.

Assume $A$ holds. I know that $A$ and $A \rightarrow B$ hold, thus $B$ holds. I know that $B$ and $B \rightarrow C$ hold, thus $C$ holds.

Assuming $A$, I showed $C$. Thus $A \rightarrow C$ holds.

Seems almost too simple. Is this a correct way to proceed?

Answer 1

Short answer: Your proof is correct and well-written.

---

Longer answer: Depending on how far you wish to take this question there are varying degrees of complexity to which an answer may exhibit. This all depends on what you allow yourself to assume. Namely, you take for granted that $A$ and $(A \implies B)$ together mean that $B$ is $\operatorname{True}$ (and you do the same for $B$ and $C$). This is, of course, intuitively obvious but you have not mathematically justified it.

This property is referred to as Modus Ponens and you can refer to this as a justification for why you were able to conclude that $B$ holds. However, you may already be thinking that this doesn't answer the question of why the property holds.

If you are familiar with the following implications: $$\operatorname{True} \implies \operatorname{True}$$ $$\operatorname{True} \newcommand{\notimplies}{\;\not\!\!\!\implies} \notimplies \operatorname{False}$$ $$\operatorname{False} \implies \operatorname{True}$$ $$\operatorname{False} \implies \operatorname{False}$$

Then you can put these into a Truth Table as follows:

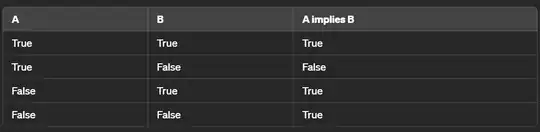
Now you can simply interchange the second and third columns to see that Modus Ponens does indeed hold. However, you may choose to question why this Truth Table holds. Again, this is something that you are likely to find intuitively true, but what is the mathematical justification for this? For that, the answer depends on how you are defining $ \implies$ and the proof can then become significantly more complicated depending on where you choose to start. See the answers to this question for two different characterisations of $\implies$ (note that these are two of the simpler constructions and you can go a lot deeper than this).

And we can continue down an (almost) neverending rabbit hole, going into deeper and deeper levels of formalism. At some point, you have to stop though and consider the purpose of the exercise.

To me, the argument you gave, as I said at the beginning, is completely correct and fine. Although, this is a question where you have the liberty to make it as easy or as complicated as you like.

Answer 2

There's a somewhat different way, arguably more intuitive. Use $p \implies q \iff q \lor \lnot p$

So we can rewrite the problem as $A \land (A \implies B) = A\land (B \lor \lnot A)$

So whereas modus ponens allows us to conclue B for the expression on the left, the right states that if A is a given, then the resulting truth value is $B \lor \lnot A$. But we are assuming A so $\lnot A$ is false. $B \lor \lnot A$ can only be true if B is true given A is true. So just as on the left, on the right we can conclude B.

A lot of implications make more sense when broken up into and/or statements.

Answer 3

$$(b \lor \lnot a) \land (c \lor \lnot b)$$

$$\equiv \left[(b \lor \lnot a) \land (c \lor \lnot b)\right]_{b=\bot} \lor \left[(b \lor \lnot a) \land (c \lor \lnot b)\right]_{b=\top}$$

$$\equiv \lnot a \lor c $$

Answer 4

This is a great thread, but I would like to reframe the question slightly. Can we prove the transitivity of implication using the equivalences of propositional logic only? That is, if we chain our premises into a statement

$((A \implies B) \land (B \implies C))$,

can we transform the statement into our conclusion

$(A \implies C)$?

@JMP proposed such a proof, but it doesn't show the key reduction (implicit on both sides of his middle step) from

$(\neg A \lor B \lor C)$ to

$(\neg A \lor C)$.

How do we get there? My only answer is that we can discard $B$ because $(A \implies B)$ was our premise. If my spare-marble bag has a blue marble and red marble, and I need a red marble, I just take the red marble. (But this was not an equivalence step, but a sort of brute-force absorption.)

Answer 5

To briefly lay stress on the fundamental idea: We understand by a proof in logic a finite sequence of well-formed formulas in a specified formal language. We may deviate from the strictly rigorous and precise presentation of a proof as the context and readership allow, however, we ought not to lose sight of the fundamental idea.

Now, we want to give a proof for the transitivity of implication which is traditionally also known as hypothetical syllogism. The following is one that uses Łukasiewicz's version of Hilbert's system. We have the axioms

Ax1.$\qquad A\rightarrow(B\rightarrow A)$

Ax2.$\qquad (A\rightarrow(B\rightarrow C))\rightarrow((A\rightarrow B)\rightarrow(A\rightarrow C))$

Ax3.$\qquad (\neg B\rightarrow\neg A)\rightarrow(B\rightarrow A)$

and the inference rule of modus ponens (MP): $\qquad\cfrac{A,\ A\rightarrow B}{B}$

---

1. $B\rightarrow C\tag{Hypothesis}$
2. $(B\rightarrow C)\rightarrow (A\rightarrow(B\rightarrow C))\tag{Ax1}$
3. $A\rightarrow(B\rightarrow C)\tag{MP 1, 2}$
4. $(A\rightarrow(B\rightarrow C))\rightarrow((A\rightarrow B)\rightarrow(A \rightarrow C))\tag{Ax2}$
5. $(A\rightarrow B)\rightarrow(A\rightarrow C)\tag{MP 3, 4}$
6. $A\rightarrow B\tag{Hypothesis}$
7. $A\rightarrow C\tag{MP 5, 6}$
8. $\qquad\therefore\quad A\rightarrow B,\; B\rightarrow C\vdash A\rightarrow C$