What does it mean for something to imply something else in maths? I don't think I've grasped this concept and it's making understanding theorems and proofs really difficult.
I think it might be the word 'imply' that's throwing me off. I've searched for definitions and examples, but they don't seem to make anything clearer.
A statement $A$ implies another statement $B$ (written as $A\Rightarrow B$), if from the truth of the former, it necessarily follows the truth of the latter.
Example. If I am in London, I am necessarily in England. So the statement "I am in London" implies the statement "I am in England".
On the other hand, if it is possible for $B$ to be true, while simultaneously $A$ is false, then $A$ is not implying $B$.
Example. If I am in England, I am not necessarily in London (I could be in Oxford). Hence, the statement "I am in England" does not imply the statement "I am in London".
In math, the fact that a statement $A$ implies a statement $B$ is written this way: $A \implies B$
The meaning of $A \implies B$ is defined by this truth table:
$$ \begin{matrix} A & B & | & A \implies B\\ T & T & | &T\\ T & F & | &F\\ F & T & | &T\\ F & F & | &T\\ \end{matrix} $$
That means that $A \implies $B is false only when $A$ is true and $B$ is false. In the other cases $A \implies $B is true.
So let's say I have a theorem that states "If $n$ is a multiple of $6$ then it must be a multiple of $2$" ($n$ multiple of $6 \implies n$ multiple of $2$). For this theorem to be true, if you encounter a multiple of $6$ then it must be also a multiple of $2$ because if not the implication would be false. But if you encounter a number that is not a multiple of $6$ then it can be a multiple of $2$ or not without invalidating the theorem, because the theorem says nothing about numbers that are not multiple of $6$.
You can also see what the implication means by looking at sets:
Update
Suppose that in a mathematical proof, proposition $Q$ can be derived from proposition $P$. This simply rules out the possibility that both $P$ is true and $Q$ is false.
$~~~~P\implies Q \space \equiv\space \neg[P\land \neg Q]$.
Note that there is also no causal relationship assumed between the antecedent $P$ and consequent $Q$, i.e. we do not assume that $P$ causes $Q$.
On causality and implication, see my recent posting: Does 'imply' in mathematics indicate causality?
I'm not sure we need another answer here. But most of the other answers follow classical logic closely. I think the constructive logic meaning may be more intuitive. It's simply:
We say that $A$ implies $B$ if any proof of $A$ can be turned into a proof of $B$
This completely evades any question about what it means for something to be “true”. It's concerned with the much more concrete and limited notion of provability.
It's a good definition because it does exactly what we want implication to do. The primary use of implication — one could argue the only use — is that if we are trying to prove $B$, then it is sufficient to prove some $A$ and also that $A$ implies $B$ (whatever that means).
The constructive definition of implication captures that purpose exactly. “$A$ implies $B$” means that we have a way to convert our proof of $A$ into a proof of $B$.
If you take two statements $P$ and $Q$ then saying "$P$ implies $Q$" or equivalently $P \implies Q$ means that if $P$ holds then $Q$ holds. For instance, the following are some factual implications.
"$x$ is a real number greater than zero" implies "$(-1)\cdot x$ is a real number less than zero." This is true because if the first statement holds then one may conclude the second holds as well.
"x is an odd number" implies "There exists a natural number $k$ such that $x = 2k + 1$." Again, from the first statement one can conclude the second.
Here is an example of an incorrect implication:
Fundamentally, mathematics is a guide to reducing the unknown. When we have a statement "If $P$ then $Q$", that means if we somehow already know that $P$ is true, then we now can be assured that $Q$ is true. Each theorem that proves an implication allows us to expand our knowledge of true facts by using chains of implications. We start with known supposed true facts and, using chains of implications, we can conclude many other true facts on the basis of the suppositions. And finally arriving at what we want to prove to be true also. The Achilles' heel of this method is that we are dependant of the starting true facts, and if any one of them turns out to be false, then the results of our implications are now not assured to be true. Another weakness is that we could make several kinds of errors in applying the implications because "to err is human" and "a chain is as strong as its weakest link".
It means the same as it means in regular English. If we say “A implies B”, it means that the truth of B is a consequence of the truth of A.
There are many different ways of expressing this. For example
And so on.
In logic, the sentence $\boldsymbol{\text‘P}$ implies $\boldsymbol {Q\text’}$ just means that $\boldsymbol P$ being true necessitates that $\boldsymbol Q$ is true.
(In particular, the assertion $\text‘P$ implies $Q\text’$ with $P$ being false allows us to deduce neither that $Q$ is true nor that $Q$ is false. Therefore, regardless of $Q$'s truth value, whenever $\boldsymbol P$ is false, it must be the case that $\boldsymbol P$ implies $\boldsymbol Q.)$
Implication statements, being underpinned by material implication, do not express causation, modality, or counterfactuals.
For example, it is true that 2 is an even number implies that Earth's moon is not made of cheese.
The statement x > 12 implies that x > 10 is not a genuine example of $\text‘P$ implies $Q\text’,$ but an example of the universal implication $\text‘\boldsymbol{\forall x\,(P(x)}$ implies $\boldsymbol{Q(x))}\text’,$ where the condition and consequent are linked by the variable $x,$ every value of which is to satisfy the statement. A visual explanation:
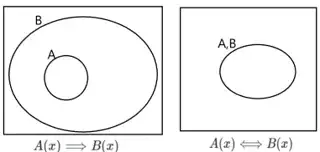
Note that truth is relative to the context. Typically, underpinning implication statements, like the last two, are various definitions (e.g., what ‘a > b’ means), axioms and/or real-world knowledge; these tacit assumptions are part of the aforementioned context, and enable us to legitimately assert implications between statements that may not be ostensibly related.
Other implication statements require none of these contexual assumptions and are true by virtue of their logical form; they are specifically called logical implication. Examples of such strong assertions are Jammy is both kerplung and zingsty implies that Jammy is not neither kerplung nor zingsty and ∀x (x>5 implies that x>5 or x<9), which are true irrespective of what ‘kerplung’, ‘zingsty’, ‘>’ and ‘<’ mean).
Roughly speaking, a logical truth is a sentence that is true regardless of how its non-logical symbols are interpreted. So, logical truths, including logical implications, are context-insensitive.
We can then classify implication into four categories:
The (non-quantified) statement I am holding a pen implies that it is raining outside (whose specific context might tacitly be right now, in Ximending, Taipei) is asserting neither causation nor a timeless truth, and is not predicting that it will rain whenever you hold a pen. It is indeed false in some context(s), since it isn't logically true.
On the other hand statement, this statement is logically true (true in every imaginable context), in other words, a logical validity: I am holding a pen and every empty-handed person is holding no object implies that I am not empty-handed.
Blockquote 5 > 4. This implies: 5 > 3, 5 > 2, and 5 > 1. If any of those statements after the first is useful in a proof, you are allowed to pull that statement out of thin air and use it. That use of implies is pretty confusing when you first start doing proofs, because for the first time the student is free to use what they know of numbers and counting to prove something is true. An original statement created as part of proving a hypothesis true.
– William Parrish Apr 09 '22 at 22:50