How to prove this recurrence relation for generalized "rounding up to $\pi$"?

Question

The webpage Rounding Up To $\pi$ defines a certain "rounding up" function by an extremely simple procedure:

Beginning with any positive integer $n$, round up to the nearest multiple of $n-1$, then up to the nearest multiple of $n-2$, and so on, up to the nearest multiple of $1$. Let $f(n)$ denote the result.

E.g., using an obvious notation, the sequence starting with $n=10$ is $$ 10 \xrightarrow{9} 18 \xrightarrow{8} 24 \xrightarrow{7} 28 \xrightarrow{6} 30 \xrightarrow{5} 30 \xrightarrow{4} 32 \xrightarrow{3} 33 \xrightarrow{2} 34 \xrightarrow{1} 34 =:f(10). $$

The interesting thing is that, according to the webpage$^\dagger$, $(f(1),f(2),f(3),\dots)$ is the same sequence that results from a certain sieving method, for which Erdős & Jabotinsky (1958) proved that $$ \lim_{n\to\infty}\frac{n^2}{f(n)} = \pi, $$

so one naturally wonders what happens if, instead of rounding up to the nearest multiple, we round up to the second-nearest multiple, or the third-nearest, etc. Thus, let $f_k(n)$ denote the result of the "rounding up" sequence when using the $k^{\mathrm{th}}$-nearest multiple; e.g., using the second-nearest multiple, the sequence beginning with $10$ is $$ 10 \xrightarrow{9} 27 \xrightarrow{8} 40 \xrightarrow{7} 49 \xrightarrow{6} 60 \xrightarrow{5} 65 \xrightarrow{4} 72 \xrightarrow{3} 75 \xrightarrow{2} 78 \xrightarrow{1} 79 =: f_2(10). $$

(These $f_k$ sequences occur in the OEIS under names like "Generalized Tchoukaillon (or Mancala, or Kalahari) solitaire" or related sieving processes, e.g. at the links $f_1$, $f_2$, $f_3$, $f_4$.)

Now let $g_k(n):={n^2/f_k(n)}$ and, assuming all the limits exist, define the sequence $(G_k)_{k=1,2,3,\dots}$ as $$ G_k := \lim_{n\to\infty} g_k(n) = \lim_{n\to\infty}\frac{n^2}{f_k(n)}. $$

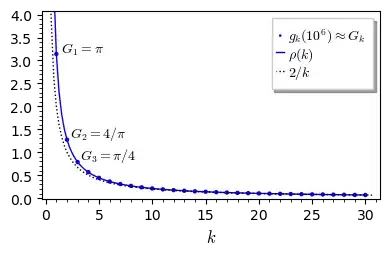
Here's a plot of $(g_k(10^6))_{k=1,\dots,30}$ in which the $g_k$ have apparently converged in at least their first $5$ digits (numerically, it appears that generally the first $d$ digits of $g_k(10^{d+1})$ are those of the limit $G_k$):

We know that $G_1=\pi,$ and in the plot I've indicated my conjectured values for $G_2,G_3$ as well, based on a simple pattern that I found by searching numerically among the $g_k(n)$; specifically, I found that $g_{k+1}(n) \approx \frac{4}{k^2\,g_k(n)}$, with the absolute error bounded by $5/n$, i.e., $$ \left|g_{k+1}(n) - \frac{4}{k^2\,g_k(n)}\right| < \frac{5}{n}, \quad k=1,2,3,\dots $$ and also that $$ \left|g_{k}(n) - a_k\right| < \frac{5}{n}, \quad k=1,2,3,\dots $$ with the $a_k$ defined recursively by $a_1=\pi,\; a_{k+1}=\frac{4}{k^2\,a_k},\; k=1,2,3,\dots$ This strongly suggests the following ...

Conjecture: $$ \boxed{\quad G_1 = \pi, \quad G_{k+1} = \frac{4}{k^2\,G_k}, \quad k=1,2,3,\dots \quad}\tag{1} $$

i.e., $$ (G_k)_{k=1,2,3,\ldots} = \left(\pi,\, \frac{4}{\pi},\, \frac{\pi}{4},\, \left(\frac{2}{3}\right)^2 \frac{4}{\pi},\, \left(\frac{3}{4} \frac{1}{2}\right)^2 {\pi},\, \left(\frac{4}{5} \frac{2}{3}\right)^2 \frac{4}{\pi},\, \left(\frac{5}{6} \frac{3}{4} \frac{1}{2}\right)^2 {\pi},\,\ldots \right). $$

Question: How to prove the recurrence relation in (1)??

NB: From the conjecture (1) it's straightforward to derive the following formulas that hold for all positive integers $k$:

$$G_k=\begin{cases}\left(\prod_{j=1}^{k-1\over 2}{2j-1\over 2j}\right)^2\pi&\text{if $k$ is odd}, \\ \left(\prod_{j=1}^{k-2\over 2}{2j\over 2j+1}\right)^2 {4\over\pi}&\text{if $k$ is even}\end{cases}\\ $$

$$G_k=\left({(k-2)!!\over(k-1)!!}\right)^2\cdot \begin{cases} \pi&\text{if $k$ is odd},\\[3ex] {4\over\pi}&\text{if $k$ is even}\end{cases}\\ $$

$$G_k\sim{2\over k}$$

where the last line is from the known asymptotic behavior of double factorials.

EDIT: As noted in a comment by Ash Malyshev, the conjectured $(G_k)_{k=1,2,3,\dots}$ can also be written compactly as a ratio of squared gamma functions that I'll call $\rho(k)$:

$$G_k = \left({\Gamma\left({k\over 2}\right) \over \Gamma\left({k+1\over 2}\right)}\right)^2=:\rho(k)$$

This can be established either by deriving it from the above formulas, or by showing that $\rho(k)$ satisfies the defining recursion (1). I've updated the above plot to include the continuous function $\rho$ (blue curve) on the real interval $(0, 30]$: The conjecture is that the blue dots ($G_k$) coincide with this curve at every positive integer $k.$

EDIT: Yet another form in which this can be written is the infinite continued fraction $$\begin{align*}G_k= \cfrac{4}{x+\cfrac{1^2}{2x+\cfrac{3^2}{2x+\cfrac{5^2}{2x+\ddots}}}} \end{align*}$$ where $x=2k-1$. This follows from the identity $$x+{1^2\over2x+}\,{3^2\over2x+}\,{5^2\over2x+}\,\cdots=4\left({\Gamma({x+3\over4})\over\Gamma({x+1\over4})}\right)^2,\quad x>0$$ which [Perron, Die Lehre von den Kettenbruchen, Band II, 1957, p.36] attributes to Ramanujan (and to Euler for selected values of $x$).

$^\dagger$ The "rounding up" function $f$ is actually implicit in the proof given by Erdős & Jabotinsky; see this answer by Misha Lavrov for more detail.

---

For reference, here is the program I used for $f_k(n)$:

# Python
def f(k,n):   
    y = n
    for x in range(n-1,0,-1):  # i.e., for x = n-1, n-2, ..., 1
        y = ((y-1)//x + k)*x   # i.e., y <- k-th multiple of x not less than y
    return y

Also, in view of the possible relevance of sieves for proving conjecture (1), here is a program implementing the following algorithm, which I claim generates the $f_k$:

Starting with seq$_1$ = $(1,2,3,\dots)$, let seq$_{i+1}$ be the result of deleting from seq$_i$ the first $k−1$ elements and then deleting every $(i+1)$th element from those remaining. $f_k(n)$ will be the first element of seq$_n.$

def sieve(k, maxel):  # generates f_k(1), ..., f_k(n) <= maxel 
    seq = list(range(1, maxel+1))   # seq_1 = (1,2,3,...,maxel)
    keep = seq[:1]    # keep the first element of seq_1
    i = 1
    while seq:        # while seq is not empty
        del seq[:k-1]   # delete the first k-1 elements
        del seq[::i+1]  # delete remaining elements with index divisible by i+1
        keep += seq[:1] # keep the first element of seq_(i+1)
        i += 1
    return keep

Answer 1

Let me offer a direct adaptation of that of Rounding up to Pi. Fix $k\geq 1$, and apply the "rounding up" algorithm by selecting the $k$-th nearest multiple, as you describe: this gives us an integer $S_{n,k}(x)$ for every integer $x$ between $1$ and $n$, such that $S_{n,k}(1) = f_k(n)$ and $S_{n,k}(n) = n$.

Most of the trajectory is a sequence of parabola

I start with the observation that the function $$ P_j(x) = (A_j - j x) x $$ coincides with $S_{n,k}$ for small values of $x$ when we choose $j=k$ and $A_k = kn+1$. Rounding up to Pi went on to construct the $A_j$ so that for every $x$, there was one $P_j$ such that $S_{n,1}(x) = P_j(x)$. Keeping with that spirit, we can in fact prove a very similar claim:

Claim 1: for every $n>k$, there exists $k\leq J,X\leq n$ and three $\mathbb{N}$-valued sequences:

• $(j_x)_{X\leq x \leq n}$ with steps in $\{0,-1\}$ and $j_n = k$,
• $(x_l)_{k-1 \leq l \leq J}$ decreasing with $x_{k-1} = n$ and $x_J = X-1$,
• and $(A_l)_{k\leq l \leq J}$ increasing

such that $$ \forall k\leq j \leq J \ , \ \forall x_j < x \leq x_{j-1} \ , \quad S_{n,k}(x) = P_j(x) . \qquad (0)$$

In other words, every $x$ with $X \leq x \leq n$ is "on the parabola $P_{j_x}$" in the sense that $S_{n,k}(x) = P_{j_x}(x)$, and the $x$ that are on the parabola $P_j$ are the integers in $(x_j, x_{j-1}]$.

proof. We start with the following observation: for every $ux < y \leq ux+x$ with $u,x,y$ integers, rounding up $y$ to the $k$-th nearest multiple of $x$ gives $(u+k)x$.

We will prove $(0)$ together with the property $$ \forall k\leq j \leq J \ , \ \forall x_j \leq x < x_{j-1} \ , \quad x(j-k) < A_j - j(x+1) \leq x(j-k+1) . \qquad (0’)$$

We have $(0)$ and $(0)’$ for $x=n$. Let us now proceed by induction. Assume that for some $0< x \leq n$, we have constructed $(j_z)_{x\leq z \leq n}$, $(x_l)_{k\leq l \leq j_x}$ and $(A_l)_{k\leq l \leq j_x}$ so that $(0)$ and $(0’)$ hold when (only there!) pretending that $x_{j_x-1} = x-1$. Write $j=j_x$.

We know that $S_{n,k}(x) = P_j(x) = x (A_j - jx) = (x-1)(A_j-jx) + (A_j-jx)$. We want to round $S_{n,k}(x)$ up to the $k$-th closest multiple of $x-1$. Observe that $A_j-jx > (x-1)(j-k)$ either from $(0’)$ (if $x<n$) or a direct computation (if $x=n$). There are three cases, depending on the value of $A_j - jx$ as it appears in $(0’)$:

• First case, $(x-1)(j-k) < A_j - jx \leq (x-1)(j-k+1)$: then $$ (x-1)(A_j - jx + j - k) < S_{n,k}(x) \leq (x-1)(A_j - jx + j - k + 1) , $$ so by the observation $S_{n,k}(x-1) = (x-1)(A_j - j(x-1)) = P_{j}(x-1)$. This proves $(0)$ and $(0’)$ for $x-1$, by setting $j_{x-1} = j$.

• Second case, $(x-1)(j-k+1) < A_j - jx \leq (x-1)(j-k+2)$: then set $j_{x-1} = j+1$, $x_j = x-1$, and observe that similarly $$ S_{n,k}(x-1) = (x-1)(A_j - j(x-1) + 1) = (x-1)(A_{j+1} - (j+1)(x-1)) $$ when we choose $A_{j+1} = A_j + x = A_j + x_j + 1$.

• Third case, $A_j - jx > (x-1)(j-k+2)$: then set $J = j$, $X=x$, $x_j = x-1$ and stop. Note that by $(0’)$ this can happens only if $j\geq x$. $\square$

Note: We can in fact guess that $J \approx \mathrm{cste} \, n^{2/3}$, as I did in a previous version, by using the approximation $X \approx A_J / 2J$, $A_J \approx n b_J$ and $X \approx J$.

Computing the parameters of the parabola

We already established in the proof that $$ A_k = kn+1 \quad , \quad A_{j+1} = A_j + x_j + 1 . $$ What is the value of $x_j$ for $k\leq j < J$? By $(0’)$ we must have $$\begin{cases} A_j-j(x_j+2) \leq (x_j+1)(j-k+1) &\iff A_j - j + k - 1 \leq (2j-k+1)x_j , \\ A_j-j(x_j+1) > x_j(j-k+1) &\iff A_j - j > (2j-k+1)x_j . \end{cases}$$ This implies $$ \left| x_j - \frac{A_j}{2j-k+1} \right| < 1 . $$ It is tedious to get exact values, so we will work with approximations instead. Define $$ B_k = A_k = kn+1 \quad , \quad \forall j\geq k \ , \ B_{j+1} = B_j + \frac{B_j}{2j-k+1} = B_j \frac{2j-k+2}{2j-k+1} . $$ We can check that $|B_j - A_j|$ is bounded for every $j$ by something independent of $n$. On the other hand, $B_j / n \to b_j > 0$ as $n\to\infty$ with \begin{align} b_{j} &= k \prod_{l=k}^{j-1} \frac{2l-k+2}{2l-k+1} = k \prod_{l=k+1}^{j} \frac{2l-k}{2l-k-1} \\ &= k \frac{\left(1+\frac k 2\right)^{(j-k)}}{\left(\frac{k+1}2\right)^{(j-k)}} = k \frac{\Gamma\left(1+\frac k 2+(j-k)\right)}{\Gamma\left(1+\frac k 2\right)} \frac{\Gamma\left(\frac{k+1}2\right)}{\Gamma\left(\frac{k+1}2 + j-k\right)} \end{align} so $A_j / n \to b_j$ as $n\to\infty$ as well. Using that $\frac{\Gamma(x+1)}{\sqrt{x}\Gamma(x+1/2)} \to 1$ as $x\to\infty$ we find that $$ \frac{b_j}{\sqrt{j}} \underset{j\to\infty}\longrightarrow k \frac{\Gamma\left(\frac{k+1}2\right)}{\Gamma\left(1+\frac k 2\right)} = 2\frac{\Gamma\left(\frac{k+1}2\right)}{\Gamma\left(\frac k 2\right)}, $$ so that as $j\to\infty$ $$ \frac{4 j}{b_j^2} \to G_k. $$

Claim 2: the sequence $(b_j / \sqrt{j})_{j\geq k}$ is monotone increasing.

This is a consequence of the log-convexity of the Gamma function.

The final value

The heuristic used in Rounding up to Pi is $$ f_k(n) := S_{n,k}(1) = \sup_{k\leq l\leq j} \sup_{1\leq x \leq n} P_l(x) . \qquad (*) $$ Let us get a precise version: since $S_{n,k}$ is decreasing and $S_{n,k}(x-1) \leq S_{n,k}(x) + k(x-1)$, we have for every $1\leq x \leq n$ $$ S_{n,k}(x) \leq f_k(n) \leq S_{n,k}(x) + k\frac{x(x-1)}{2} . $$ We have constructed the sequences of Claim 1 for at least all $j\leq J$, where $J = j_X$ and $X$ is the largest integer such that $j_X \geq X$. Since $j_X \leq k + (n-X)$ we must have $J\geq c \sqrt{n}$ for some $c>0$, implying $J\to \infty$ as $n\to\infty$.

We can find functions $r_1, r_2, \dots$ such that for every $j < J$, $$|A_j - n b_j| \leq r_1(j) \quad , \quad \left| x_j - \frac{n b_j}{2j-k+1} \right| \leq r_2(j) \ , $$ which implies (recalling $S_{n,k}(x_j+1) = P_j(x_j+1)$) $$ \left| S_{n,k}(x_j+1) - n^2 b_j^2 \frac{j-k+1}{(2j-k+1)^2} \right| \leq n r_3(j) . $$ Take now any $j$ fixed and arbitrarily large; because $J\to\infty$ as $n\to\infty$ we will have $j<J$ for every $n$ large enough, and the above inequalities will be verified. This gives us, first that $$ \liminf_{n\to\infty} \frac{f_n(k)}{n^2} \geq \liminf_{n\to\infty}\frac{S_{n,k}(x_j+1)}{n^2} \geq b_j^2 \frac{j-k+1}{(2j-k+1)^2} $$ where the right-hand side is larger than $G_k^{-1}-\epsilon$ for every $j$ large enough; then that \begin{align} \limsup_{n\to\infty} \frac{f_n(k)}{n^2} \leq \limsup_{n\to\infty} \left(\frac{S_{n,k}(x_j+1)}{n^2} + k\frac{x_j(x_j-1)}{2n^2}\right) \leq b_j^2 \left( \frac{j-\frac{1}{2}k+1}{(2j-k+1)^2} \right) \end{align} which by the same reasoning is smaller than $G_k^{-1} + \epsilon$ for every $j$ large enough. This concludes the proof of the convergence $$ \frac{n^2}{f_k(n)} \underset{n\to\infty}\longrightarrow G_k , $$ with $G_k$ given by your formulas.

Edits

Edit 1: Some mistakes have slipped in my final computations. I rewrote $b_j$ using Pochhammer symbols and Gamma functions, which makes computation easier afterwards.

Edit 2: Added a proof of the heuristic (*).

Edit 3: Major rewrite, with division into sections. I have tried to made things less informal: many back-of-the-envelope calculations are now almost-rigorous, at the cost of the technical Claim 1.

Edit 4: Added a proof of Claim 2.

Edit 5: Corrected the final proof of the convergence of $f_k(n)$ by bounding the difference between $f_k(n)$ and $S_{n,k}(x_j+1)$ for any fixed $j$.