Motivation
Lemma. $h_n(x) = \sum\limits_{d \mid p_n\#}(-1)^{\omega(d)} \sum\limits_{r^2 = 1 \pmod d} \left\lfloor \frac{x - r}{d}\right\rfloor$ counts the number of twin prime averages in the interval $[p_n +2, x]$ for all $p_n + 2 \leq x \leq p_{n+1}^2 - 2$.
Proof. I can prove the above using elementary definitions and inequalities.
Conjecture. An affine function lower-bounding $h_n(x)$ is:
$$ f_n(x) = \frac{-n}{2} + x\sum_{d \mid p_n\#}\frac{(-1)^{\omega(d)}{\begin{cases} 2^{\omega(d) -1},2\mid d \\ 2^{\omega(d)}, \text{else} \end{cases}}}{d} $$
In other words the slope $m$ of the trend line $f_n$ is precisely the sum of all $(-1)^{\omega(d)} \frac{1}{d}$ such that $r \in$ the group $G_d = \{ r \in \{0, \dots, d-1\} : r^2 = 1\pmod d\}$ which is the same thing as above.
Evidence
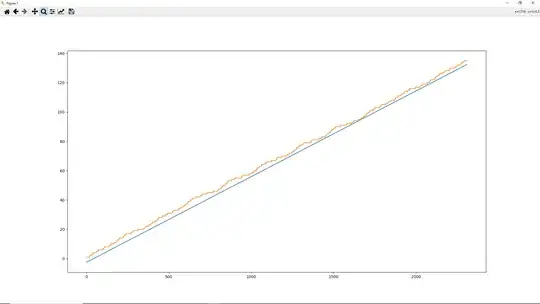
This code which generates the above screenshot showing the trend line above next to what it lower bounds, but zoomed in on the window of $X = p_{n} + 2... 2\cdot( p_{n+1}^2 - 2)$.
from sympy import *
def f(n, x, P):
S = 0
R = -(n+1)/2
Q = 0
for d in divisors(P):
T = 0
U = 0
V = 0
for r in range(0, d):
if (r2 - 1) % d == 0:
U += floor((x- r)/d)
T += (x - r)/d
V += floor((-r)/d)
S += (-1)primeomega(d) * U
R += (-1)primeomega(d) * T
Q += (-1)primeomega(d) * V
return R, S, Q
X = Symbol('X')
N =5
M = primorial(N)
S,R, Q = f(N, X, M)
print(S)
print(R)
print(f'Q={Q}')
a = prime(N+1) + 2
b = prime(N + 2)**2 - 2
delta = 1.0
n = int((b-a) / delta)
Xvals = []
Yvals = []
Xvals1 = []
Yvals1 = []
max = 0
for x in range(a, 2*(b+1)):
Xvals1.append(x)
z,y,_= f(N, x, M)
if abs(z-y) > max:
max = abs(z-y)
Yvals1.append(z)
Yvals.append(y)
print(f'Max diff = {max}')
import matplotlib.pyplot as plt
plt.plot(Xvals1, Yvals1)
plt.plot(Xvals1, Yvals)
plt.show()
It's already been proven that the slope is indeed correct, here by Bryan Moehring, even for more general sums of such step functions. In other words, any such trend line or bounding line must have a slope of that form, so that is solved for. I merely seek a constant for $b$. I think $b = -n/2$ seems like good choice. Judging by zooming in on the above $n=5$ screenshot, it's a really tight bound.
Question
How can I prove that $b = -n/2$ is sufficient so that $f_n(x) = mx + b \leq h_n(x)$ for all $x \in \Bbb{R}$? (For sufficiently large $n$)
Further Motivation
$$ \sum_{d \mid p_n\#}\frac{(-1)^{\omega(d)}{\begin{cases} 2^{\omega(d) -1},2\mid d \\ 2^{\omega(d)}, \text{else} \end{cases}}}{d} = \\ (1-\frac{1}{2})\sum_{d \mid \frac{p_n\#}{2}}\frac{(-2)^{\omega(d)}}{d} $$
So this seems like something to which we can apply Mertens' Theorems to.
If the estimate for $b$ is correct, that would mean we can expect at least:
$$ f_n(p_{n+1}^2-2) = -\frac{n}{2} + (p_{n+1}^2 -2) M $$
twin prime averages to occur in the interval $I = [p_{n} + 2, p_{n+1}^2 - 2]$. Where $M = \frac{1}{2}\sum\limits_{d \mid \frac{p_n\#}{2}}\frac{ (-2)^{\omega(d)}}{d}$. And $M$ is handled nicely by Mertens application.