Today I thought a lot about very simple population models, and there are still a few things that bug me.
Consider a simple discrete exponential growth function:
$$ n(t+1) = n(t) + n(t) b - n(t) d = n (1+r) $$
And recursively expanding the formula for an time interval $T$ yields
$$ n(T) = n_0 (1+r)^{T} \tag{Eq.1}$$
where:
- $b$ and $d$ are rates (birth and death) expressed as a proportion of the population (thus $d$ ranges from $0$ to $1$)
- $r=b-d$ is the overall growth rate including both births and death
(These things might not be relevant but I'm not sure so I'll be very explicit with the notation)
This equation comes intuitively considering that at each time the population is the same as the previous time frame plus some births minus some deaths.
Now let's consider the continuous time exponential growth.
First of all, I have not found a simple way to pass from the discrete formula to the continuous one (maybe it's not possible?).
Anyway to obtain it one could do the same type of reasoning as above, we can write
$$ \frac{dn}{dt} = bn - dn = rn$$
Because the variation in the population size should be proportional to the births and inversely proportional to the deaths.
Integrating this formula for $t$ between $t=0$ and $t$, and for $n$ between $n_0$ and $N(t)$ we obtain:
$$ N(t) = n_0 \cdot e^{rt} \tag{Eq.2}$$
Now I tried to plug some numbers in to simulate the results and I found out that they are in fact different... but shouldn't they be the representation of the same phenomenon?
Here is the plot for the 2 equations
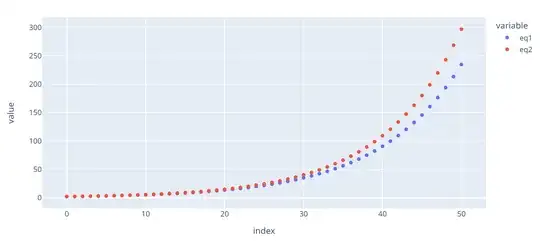
Maybe the error is thinking that r must be the same? But if so what is the relationship between the discrete and continuous $r$?