The range of $p_1$ is given by $[\alpha, \beta]$ where
$$\beta = \frac{1}{d} + \sqrt{\rho - \frac{\rho}{d} - \frac{1}{d} + \frac{1}{d^2}}$$
and
$$\alpha = \frac{1}{m} + \frac{1}{m}\sqrt{\frac{m\rho - 1}{m-1}}$$
where $m = \lfloor 1/\rho\rfloor + 1$.
Moreover, $p_1 = \beta$ if $p_2 = p_3 = \cdots = p_d = \frac{1}{d} - \frac{1}{d}\sqrt{\frac{d\rho - 1}{d-1}}$;
$p_1 = \alpha$ if
$p_1 = p_2 = \cdots = p_{m-1} = \alpha$
and $p_m = \frac{1}{m} - \sqrt{\rho - \frac{\rho}{m} - \frac{1}{m} + \frac{1}{m^2}}$ and $p_{m+1} = \cdots = p_d = 0$.
Proof:
(1) Prove that $p_1 \le \beta$
We have
$$1 - p_1 = p_2 + p_3 + \cdots + p_d
\le \sqrt{(d-1)(p_2^2 + p_3^2 + \cdots + p_d^2)} = \sqrt{(d-1)(\rho - p_1^2)}$$
or
$$-dp_1^2 + 2p_1 + d\rho - \rho - 1 \ge 0$$
which results in
$$p_1 \le \beta.$$
(2) Prove that $p_1 \ge \alpha$
Let $y_1 = y_2 = \cdots = y_{m-1} = \alpha$ and $y_m = \frac{1}{m} - \sqrt{\rho - \frac{\rho}{m} - \frac{1}{m} + \frac{1}{m^2}}$ and $y_{m+1} = \cdots = y_d = 0$.
If $p_1 < \alpha$, then
$(p_1, p_2, \cdots, p_d)$ is majorized by
$(y_1, y_2, \cdots, y_d)$.
By Karamata's inequality,
we have
$$p_1^2 + p_2^2 + \cdots + p_d^2
< y_1^2 + y_2^2 + \cdots + y_d^2 = \rho.$$
This is impossible.
We are done.
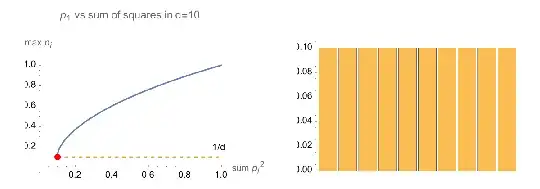

so we can see that $ |p_1| \geq \sqrt{\frac{\rho}{d}}$.
– Doge Chan Feb 05 '23 at 20:31