Question: If the wire of length is cut into three pieces then the probability that the three pieces form a triangle is ____
My approach is as follow
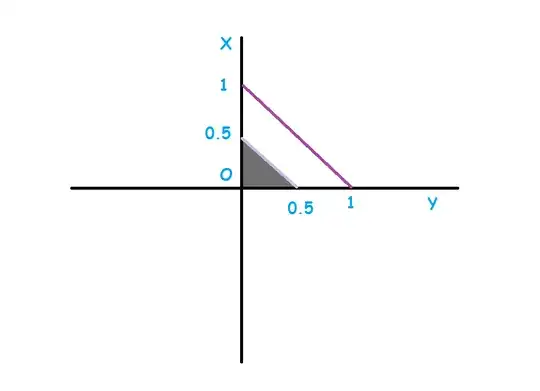
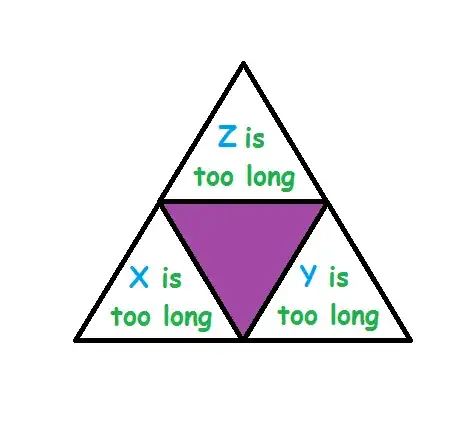
For a triangle to exist the sum of two sides should be greater than the third side
Hence $x + y + z = \ell \Rightarrow z = \ell - \left( {x + y} \right) > 0$
$x > 0,y > 0,z > 0$
$x + y > z \Rightarrow x + y > \ell - \left( {x + y} \right) \Rightarrow x + y > \frac{\ell }{2}$
$y + z > x$ & $y + z > \frac{\ell }{2}$
$z + x > y$ & $z + x > \frac{\ell }{2}$, therefore $x + y + z > \frac{{3\ell }}{4}$
How do we proceed further