Motivation
I'm contemplating about what is the geometric property whose special case would be the property of $\mathop{epi}(f)$ for a function $f$ with $f^{(3)}\geq 0$, akin to convexity being the special case of the property of $\mathop{epi}(f)$ for $f$ with $f''\geq 0$? (Note that $S=\mathop{epi}(f)$ of a convex function besides for being convex is such that $S+\{0\}\times \Bbb R_+ = S$, so convexity is indeed a more general property than the one that $\mathop{epi}(f)$ satisfies.)
Consider the following definitions:
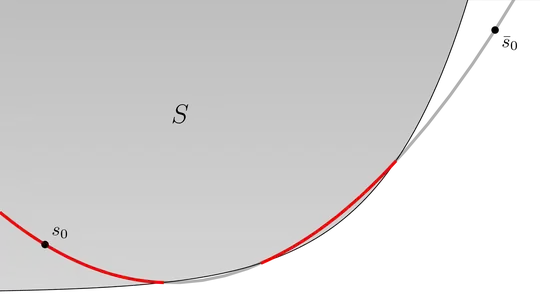
Definition 1: We say that a set $S\subset \Bbb R^2$ is second order start-convex with respect to points $s_0\in S, \bar s_0 \in \Bbb R^2 \setminus S$ if for any conic $C$ containing both $s_0$ and $\bar s_0$ the set $S \cap C$ consists of at most 2 connected sets (in the sense that two branches of hyperbola are regarded as a connected curves).
In intuitive terms, any conic passing through both $s_0$ and $\bar s_0$ can not "reenter" $S$ twice.
Definition 2: We say that a set $S\subset \Bbb R^2$ is second order start-convex with respect to line $L\ni (0,0)$ if for any parabola $P$ with the axis of symmetry parallel to $L$ the set $S \cap P$ consists of at most two connected curves.
In intuitive terms, any parabola with the axis of symmetry parallel to $L$ can not "reenter" $S$ twice.
Questions
- Is there an established term for what I call second order start-convex set?
- How to make Definition 2 a special case of Definition 1 for a special choice of points $s_0,\bar s_0$. (In my understanding all the parabolas with axis of symmetry parallel to a line $L$ have two points at the infinity in common, but I'm struggling formulating it.)
Analogy
A star-convex set can be similarly characterized as follows:
A set $S\subset \Bbb R^2$ is start-convex with respect to the vantage point $s_0 \in S$ if for any line $L$ passing through $s_0$ the set $S \cap L$ is connected.