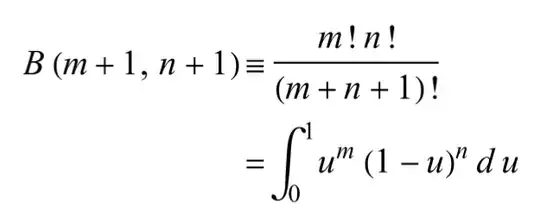3

In Jack's answer here, they have the integral $$\int_{0}^{1}\left(-1+\frac{1}{\sqrt{1-u^2}}\right)\frac{du}{u^{3/2}}$$ to which they claim can be evaluated using the substitution $s=u^2$ and the Beta function.

When I perform the substitution, I get the integral $$\frac12\int_0^1\left(-1+(1-s)^{-\frac12}\right)\cdot s^{-\frac54}ds$$

I have spent several hours now attempting to find a way to convert this form to a Beta function, but the definitions on both wikipedia and mathworld do not have this form.

The annoying part of the integrand is of course the $-1$ in the parenthesis, but no matter what I do, I cannot get rid of it. Attempting to separate it into two integrals makes both diverge. However, if I do it anyways, I get this

$$\frac12\int_0^1-s^{-\frac54}+{\color{red}{s^{-\frac54}(1-s)^{-\frac12}}}ds = \frac12\left(\text{divergent}+ {\color{red}{\operatorname{B}\left(-\frac14, \frac12\right)}}\right)$$

Even though both parts are divergent, if I follow the formula I find in mathworld

enter image description here

I get a converging value. Not only this, but this beta function value is exactly the same as part of Jack's answer below

$$\frac{1}{2} \left(4+{\color{red}{\frac{\sqrt{\pi }\Gamma\left(-\frac{1}{4}\right)}{\Gamma\left(\frac{1}{4}\right)}}}\right)$$

Surely this is a coincidence?

Regarding this, I have two questions.

  1. How do I convert the integrand into one where I can use the beta function?
  2. What is happening with the diverging values above?

Thank you!

Max0815
  • 3,584
  • 1
    $$-1+(1-s)^{-\frac{1}{2}} = \frac{s}{1-s+\sqrt{1-s}}$$ by putting over a common denominator. The divergent singularities have vanished – Ninad Munshi Jan 08 '23 at 07:50
  • @NinadMunshi how would I convert that denominator into a power of (1-s) though? – Max0815 Jan 08 '23 at 08:16

1 Answers1

2

We introduce the analytical continuation of Beta-function $\Bigl (B(\gamma,\alpha)=\int_0^1s^{\gamma-1}(1-s)^{\alpha-1}ds$, if $\gamma, \alpha >0\,\Bigr)$ for $\boldsymbol{negative}$ $\gamma\in(-1,0)$: $$B(\gamma,\alpha)=-\frac{1}{(\exp(2\pi{i}\alpha)-1)(\exp(2\pi{i}\gamma)-1)}\oint_Ps^{\gamma-1}(1-s)^{\alpha-1}ds$$

where $P$ is Pochhammer contour in the complex plane. It can be proved that analytically continued Beta-function is expressed in the usual way in terms of Gamma-function: $B(\gamma,\alpha)=\frac{\Gamma(\gamma)\Gamma(\alpha)}{\Gamma(\gamma+\alpha)}$. This expression is valid for all complex $\alpha, \gamma$.

It can also be shown that for $\gamma\in(-1;0)$ and $\alpha>0$ $$B(\gamma,\alpha)=\lim_{r\to0}(\int_r^1s^{\gamma-1}(1-s)^{\alpha-1}ds+\frac{r^\gamma}{\gamma})$$ (You can have a look, for example, here - I apologise for a clumsy explanation, but I did not manage to find this theme in an appropriate form in open sources).

The rest is straightforward: $$J(\gamma,\alpha,\alpha')=\int_0^1s^{\gamma-1}\left((1-s)^{\alpha-1}-(1-s)^{\alpha'-1}\right)ds$$$$=\lim_{r\to0}\int_r^1s^{\gamma-1}\left((1-s)^{\alpha-1}-(1-s)^{\alpha'-1}\right)ds=\lim_{r\to0}\left(B(\gamma,\alpha)-\frac{r^\gamma}{\gamma}-B(\gamma,\alpha')+\frac{r^\gamma}{\gamma}\right)$$ $$J(\gamma,\alpha,\alpha')=B(\gamma,\alpha)-B(\gamma,\alpha')$$ In your case $$I=\frac12\int_0^1\left(-1+(1-s)^{-\frac12}\right)\cdot s^{-\frac54}ds=\frac{1}{2}\Big(B\big(-\frac{1}{4};\frac{1}{2}\big)-B\big(-\frac{1}{4};1\big)\Big)$$ $$=\frac{1}{2}\bigg(\frac{\Gamma\big(-\frac{1}{4}\big)\Gamma\big(\frac{1}{2}\big)}{\Gamma\big(\frac{1}{4}\big)}-\frac{\Gamma\big(-\frac{1}{4}\big)\Gamma(1)}{\Gamma\big(\frac{3}{4}\big)}\bigg)$$ Using the main property of the Gamma-function $$\Gamma\Big(1-\frac{1}{4}\Big)=-\frac{1}{4}\Gamma\Big(-\frac{1}{4}\Big)\,\Rightarrow\,\Gamma\Big(-\frac{1}{4}\Big)=-4\,\Gamma\Big(\frac{3}{4}\Big)$$ and the relation $$\Gamma\big(\frac{3}{4}\big)\Gamma\big(\frac{1}{4}\big)=\frac{\pi}{\sin\frac{\pi}{4}}=\sqrt2\,\pi$$ $$I=\frac{1}{2}\bigg(4-4\frac{\Gamma\big(\frac{3}{4}\big)\sqrt\pi}{\Gamma\big(\frac{1}{4}\big)}\bigg)=2\bigg(1-\frac{\Gamma^2\big(\frac{3}{4}\big)}{\sqrt{2\pi}}\bigg)$$

Svyatoslav
  • 20,502