7

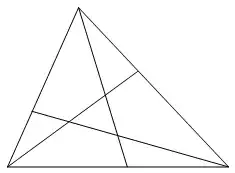
In a triangle, lines are drawn from each vertex to the opposite side. Can there be seven regions of integer area?

enter image description here

Context

My question was inspired by a similar question, which asks if a triangle is inscribed in a circle, can the four regions have integer area?

My attempt

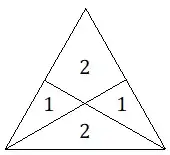
I started by considering a simpler question: In a triangle, two lines are drawn, each one from a vertex to the opposite side. Can there be four regions of integer area? The answer is clearly yes. For example, if the triangle is equilateral, and the two lines go through the centre, then we can have four regions of area $1, 1, 2, 2$:

enter image description here

But when I consider three lines (and seven regions), the situation seems to be much more complicated, and I have not found a feasible approach.

Dan
  • 35,053

1 Answers1

12

Of course there can! To see why, take the points of the large triangle to have any rational coordinates. Let the lines all have rational slope and y-intercept. Then all points are rational and thus by the shoelace formula, all the areas are rational. Since the areas are all rational, they share a common denominator. Enlarge the figure by this common denominator, and all areas are then integers.

TheBestMagician
  • 3,038
  • 9
  • 21