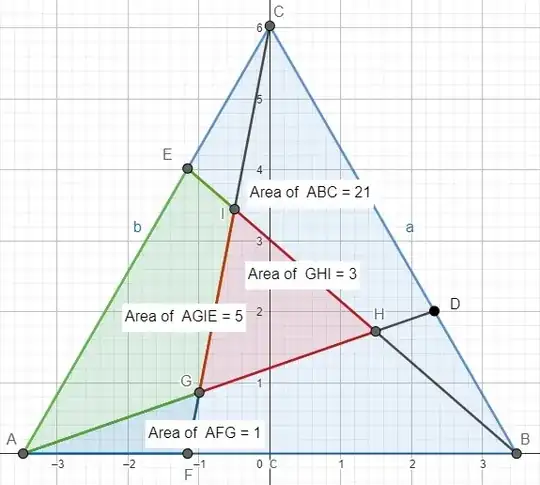
In an equilateral triangle, lines are drawn from each vertex to the opposite side. Can there be seven regions of integer area?
If we did not require that the starting triangle is equilateral, then the answer would be yes, by assuming that the starting triangle's vertices, and the points where the lines meet the sides, all have rational coordinates, and then applying the shoelace formula.
But the starting triangle is equilateral, so its vertices cannot all have rational coordinates. We can still apply the shoelace formula, but it is not obvious whether the resulting areas can all be integers.