3

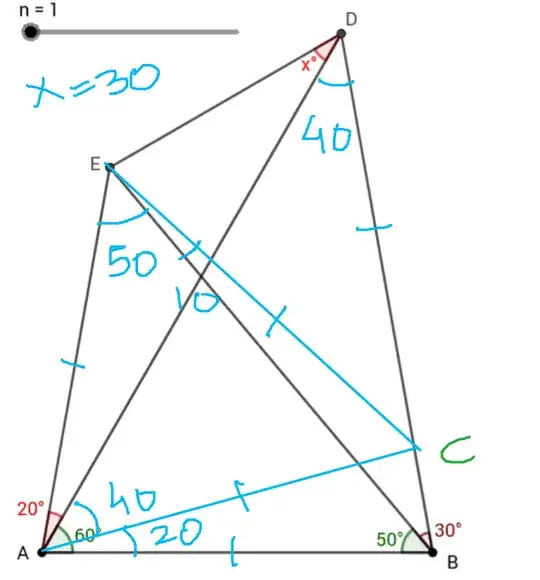
I was looking around at geometry questions and came across this Original Question

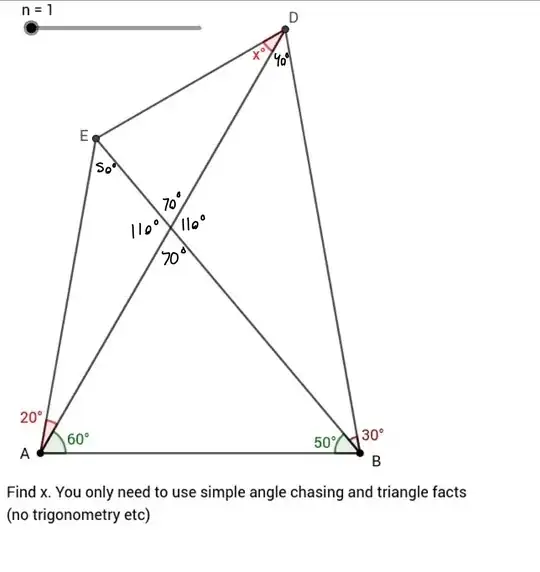
Seemed simple but I got stuck after filling in everything I knew. This is what I couldn’t get passed With filled values

Only thing I could think of doing is drawing auxiliary lines to fill values but I couldn’t think of useful ones.

Help

Siong Thye Goh
  • 153,832
SebtheSong
  • 69
  • 1
    This is a variant of "the hardest easy math problem." This link has the step by step solution. https://mindyourdecisions.com/blog/2016/09/04/the-hardest-easy-geometry-problem-sunday-puzzle/#:~:text=The%20problem%20is%20known%20as,it%20is%20difficult%20and%20laborious. – user317176 Nov 29 '22 at 07:17
  • https://en.wikipedia.org/wiki/Langley%27s_Adventitious_Angles – Jaap Scherphuis Nov 29 '22 at 08:00

2 Answers2

1

This is a fairly simple problem, here's my approach:

enter image description here

1.) Locate point $C$ on $BD$ and join it with $A$ and $E$ such that $\angle BAC=20$. Now that we know that $\angle BAC=20$ and $\angle ABC=80$, we can infer that $\angle ACB=80$, therefore $AB=AC=AE$.

2.) Since $\angle EAC=60$ and $AE=AC$, we can say that $\triangle AEC$ is equilateral, therefore $AB=AC=AE=EC$. Notice that $\angle DAC=\angle ADC=40$, therefore, $AB=AC=AE=EC=DC$. This proves that $C$ is the circumcenter of $\triangle AED$, therefore via the inscribed angle theorem, $x=30$

冥王 Hades
  • 3,112
0

Start by noticing that $ABE$ is a particular triangle. After that, draw the line parallel to $AB$ going through $E$, and the one parallel to $AE$ going through $B$. Once you are done with that, calculate the new angles with the newly formed triangles (very easy given what you already have). Then use what you know about the triangle $ABE$ to draw a very nice line going through $A$ and cutting $[EB]$ in half. Once you are done with that, observe that the triangle $OED$ (where $O$ is the point formed by the intersection of $DB$ and the line parallel to $AB$ going through $E$) is VERY SIMILAR to a newly formed triangle that you know the angles of...

Maxosaurus
  • 127