Numerical range of $A\in\mathbb{C}^{n\times n}$ is defined as $$W(A):=\{(\Re (x^*Ax),\Im(x^*Ax)) :x^*x=1\}\subseteq \mathbb{C}^2.$$ A matrix $A$ is called sectorial if $0\notin W(A).$ Let's define the following set:
$$\mathcal{A}:=\{A\in\mathbb{C}^{n\times n}: A \text{ is sectorial,}\quad |\Im(x^*Ax)|\leq|\Re(x^*Ax)|\tan\alpha, \quad \sigma(A)\in[\beta^{-1},\beta]\},$$
where $\alpha\in[0,\pi/2)$, $\beta\geq1$ and $\sigma(A)$ are the singular values of $A$.
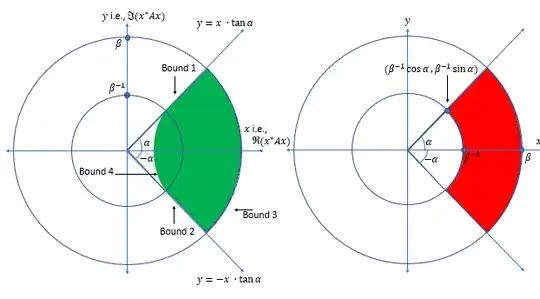
LHS of above figure shows the numerical range plot of $\cup_{A\in\mathcal{A}}W(A)$ (green region). Bounds $1,2$ and $3$ are known, however bound $4$ is not known. I am trying to find out that bound (at least partially).
If $A\in\mathrm{C}^{2\times 2}$, then $W(A)$ is an ellipse and eigenvalues of $A$ are foci of this ellipse. Eigenvalues of $A\in\mathcal{A}$ turns out always lie in red region given by RHS of above figure. I am interested in all ellipses with center at $(k,0)$ that are bound between lines $y=x\tan\alpha$, $y=-x\tan\alpha$ and circle $x^2+y^2=\beta^2$ and have foci in red region and foci are symmetric with respect to real line. I also assume that ellipses are tangent to points $(\beta^{-1}\cos\alpha, \beta^{-1}\sin\alpha)$ and $(\beta^{-1}\cos\alpha, -\beta^{-1}\sin\alpha)$. My hope is that such ellipses can give me the exact shape of bound $4$. All such ellipses were characterized here: Ellipse bounded between two lines and a circle.
Ellipse equation:
$$\frac{(x-k)^2}{a^2}+\frac{y^2}{b^2}=1$$
where
$$a=\sqrt{\frac{k(k\beta-\cos\alpha)}{\beta}}, \quad b=\sqrt{\frac{k\sin^2\alpha}{\beta\cos\alpha}}, \quad k \in \begin{cases} [\beta^{-1}\cos\alpha, \frac{\beta^3 \cos \alpha}{\beta^4 \cos^2 \alpha + \sin^2 \alpha}] & \mbox{if } \beta^2 \cos \alpha \le 1 \\ [\beta^{-1}\cos\alpha,\frac{\beta^3}{2\beta^2 -\cos \alpha}] & \beta^2 \cos \alpha > 1 \end{cases}$$
Now, assume that $\beta^2 \cos \alpha \le 1$. Then I have the following two conjectures:
Conjecture $1$: The bound $4$ is given by an ellipse that has above equation at $k=\frac{\beta^3 \cos \alpha}{\beta^4 \cos^2 \alpha + \sin^2\alpha}$.
Conjecture $2$: The smallest real point of $\cup_{A\in\mathcal{A}}W(A)$ is equal to $k-a=\frac{\beta^3\cos\alpha-\beta\cos\alpha\sin\alpha\sqrt{\beta^4-1}}{\beta^4 \cos^2 \alpha + \sin^2\alpha}$.
I am trying to prove Conjecture $2$ first. When $\alpha=0$, then $\mathcal{A}$ is a set of all positive definite Hermitian matrices with $\sigma(A)\in[\beta^{-1},\beta]$, and its numerical range is just a line, so the smallest real point of $\cup_{A\in\mathcal{A}}W(A)$ will be equal to $\beta^{-1}$, so the Conjecture $2$ is consistent. When $\beta=1$, $\mathcal{A}$ is a set of all unitary matrices with $|\Im(x^*Ax)|\leq|\Re(x^*Ax)|\tan\alpha$, so the smallest real point of $\cup_{A\in\mathcal{A}}W(A)$ will be $\cos\alpha$, which is also consistent with Conjecture $2$.
But I couldn't show that the following general inequality holds:
$$\Re (x^*Ax)\geq \frac{\beta^3\cos\alpha-\beta\cos\alpha\sin\alpha\sqrt{\beta^4-1}}{\beta^4 \cos^2 \alpha + \sin^2\alpha}\qquad \text{for all $A\in\mathcal{A}$, and all unit vectors $x$.}$$