5

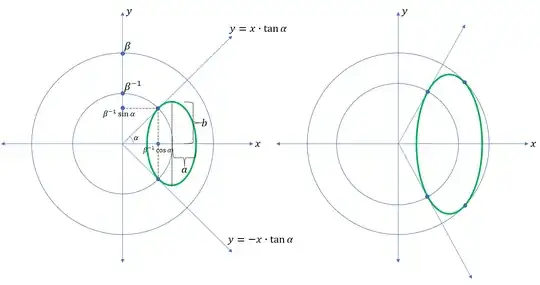
Given two circles with radii $\beta$ and $\beta^{-1}$, where $\beta\geq1$. Also, given two lines $y=x\tan\alpha$ and $y=-x\tan\alpha$, where $\pi/2>\alpha\geq0$. I am interested in all ellipses with center at $(k,0)$ that are bound between these two lines and the larger circle (LHS of Figure). I also assume that ellipses are tangent to points $(\beta^{-1}\cos\alpha, \beta^{-1}\sin\alpha)$ and $(\beta^{-1}\cos\alpha, -\beta^{-1}\sin\alpha)$, and has the following equation:

$$\frac{(x-k)^2}{a^2}+\frac{y^2}{b^2}=1.$$

enter image description here

I assume that $b\geq a$. I found that all such ellipses can be obtained by the following equations:

$$a=\sqrt{\frac{k(k\beta-\cos\alpha)}{\beta}}, \quad b=\sqrt{\frac{k\sin^2\alpha}{\beta\cos\alpha}}.$$

So, by changing $k$ in the range $[\beta^{-1}\cos\alpha, \beta^{-1}\frac{1}{\cos\alpha}]$ I can obtain all such ellipses: desmos.

However, for some combination of $\beta$ and $\alpha$, $k$ cannot reach $\beta^{-1}\frac{1}{\cos\alpha}$, since ellipse will touch larger circle before that (RHS of Figure). Given $\alpha,\beta$ pair, I want to find the largest $k$ allowed, before an ellipse touches the larger circle.

insipidintegrator
  • 6,730
Lee
  • 1,978

1 Answers1

3

Suppose the circle with radius $\beta$ and the ellipse touch at a point with co-ordinates $(x,y)$, where $y\neq 0$. Then the gradients of the two curves are equal at that point. For the circle, $x +ym = 0$ and for the ellipse, $b^2(x-k)+a^2ym=0$, where $m$ is the common gradient. This implies that $b^2(x-k)-a^2x=0$ or $(b^2-a^2)x=b^2k$. But also, this point must be on the intersection of the two curves: this gives the quadratic $$(b^2-a^2)x^2-2kb^2x+k^2b^2+a^2\beta^2 - a^2b^2$$ and, substituting for $(b^2-a^2)x$, we get $b^2kx=k^2b^2+a^2\beta^2 - a^2b^2$. Eliminating $x$ between the two expressions gives $$(\beta^2-b^2)(b^2-a^2)-k^2b^2=0.$$ Substituting into this for $a$ and $b$ in terms of $k$ gives $$(\beta^4 \cos^2 \alpha + \sin^2 \alpha)k = \beta^3 \cos \alpha.$$ This will be the maximum value of $k$, unless the $x$ value required is greater than $\beta$, in which case no point on the circle will correspond to it. Thus this condition applies when $(b^2-a^2)\beta \ge b^2k$ or $\beta^2 \cos \alpha \le 1$.

When this condition doesn't apply, there is the possibility that they touch at $(\beta, 0)$, which requires $(\beta-k)^2=a^2$; then using $a$ in terms of $k$ then gives $(2\beta^2 -\cos \alpha)k=\beta^3$ for the maximum $k$.

mcd
  • 4,231