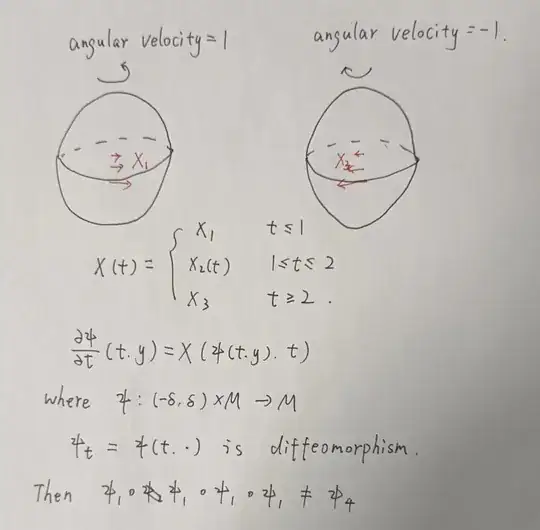In the study of solitons of Ricci flow, we need to consider a time dependent vector field $X(t)$ and the generating diffeomorphisms $\psi: \mathbb R\times M \rightarrow M$ (for detail to read the 1.2 of Lectures on the Ricci flow). And denote $\psi_t(x)=\psi(t,x)$.
They satisfy that, for any smooth function $f:M\rightarrow \mathbb R$ (where $M$ is the smooth manifold), $$ X(\psi_t(y),t)f =\frac{\partial f\circ \psi_t}{\partial t} (y) ~~~~~~y\in M \tag{1} $$ Assuming we have a local coordinate such that $$ f(x)=f(x^1,...,x^n) \\ \psi_t(x) = (\psi_t^1(x),...,\psi_t^n(x)) \\ X(\psi_t(y),t) = X^i(\psi_t(y),t) \frac{\partial}{\partial x_i} $$ then, $(1)$ is equal to $$ \frac{\partial f}{\partial x_i} (\psi_t(y)) \frac{\partial \psi_t^i}{\partial t}(y) = X^i(\psi_t(y), t) \frac{\partial f}{\partial x_i} (\psi_t(y)) $$ Therefore, the existence of $\psi_t$ is equal to the existence of $$ \frac{\partial \psi_t^i}{\partial t}(y) = X^i(\psi_t(y), t) \tag{2} $$ Although, I guess that $(2)$ may have not solution. But the key point is that I need $$ \psi_a\circ\psi_b = \psi_{a+b} \tag{3} $$ for deal the below related problem. But obviously, $(1)$ is not the usual one-parameter transformation, I don't know how to get $(3)$ ?
Related problem : How to show $\partial_t \hat g = \sigma'(t)\psi_t^* (g) + \sigma(t) \psi_t^*(\partial_t g) + \sigma(t) \psi_t^*(L_Xg)$?
PS(a few hours late): I've constructed a counterexample and write it in picture below. Where the $X_2(t)$ can be suitably choose. For example $$ X_2(t) = (2-t) X_1 + (t-1) X_3 $$ The $X_1, X_2$ are the velocity fields on $S^2$ respect to angular velocity $1,-1$. Obviously, $$ \psi_3=id\ne \psi_1\circ\psi_1\circ\psi_1$$