Can we compute this integral $\int_0^{2\pi} \frac{1}{5+3 \cos x} dx$ using an antiderivative defined on $\mathbb R$?

Question

I was trying to compute this integral $$\int_0^{2\pi} \frac{1}{5+3 \cos x} dx$$ using the substitution method $t = \tan \frac{x}{2}$ suggested in Michael Spivak's book: Calculus 3rd ed., pages 382-383. So I got the antiderivative $$\int \frac{1}{5+3 \cos x} dx = \frac{1}{2} \arctan \left(\frac{1}{2}\tan \frac{x}{2}\right)+ C$$ and then using the Fundamental Theorem of Calculus I get $$\int_0^{2\pi} \frac{1}{5+3 \cos x} dx = \frac{1}{2} \arctan \left(\frac{1}{2}\tan \frac{x}{2}\right)\Big|_0^{2\pi} = 0.$$ However, when I was checking my work in WolframAlpha I get this result:

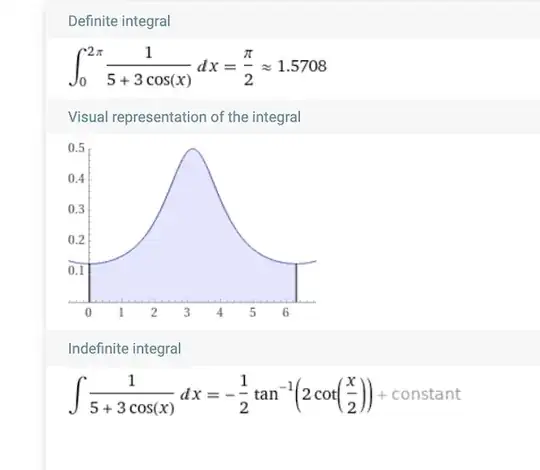
The area under the curve and the calculation from WolframAlpha makes sense to me.

One thing I noticed is that my antiderivative is not well defined everywhere, so maybe that is the reason why it does not work. But not sure :(

Update: Some members have suggested this answer: Find $\int_0^{2\pi} \frac{1}{4-5\cos x}dx$. Although it answers some of my questions, I was wondering if it is possible to compute an antiderivative defined on $\mathbb R$ that actually works without using complex analysis. :(

Can we compute the integral using an antiderivative defined on $\mathbb R$?

Edit 1: I fixed the value of the antiderivate I got.

Edit 2: Updated my question.

Edit 3: Updated my question again.

Answer 1

So with that Weierstrass substitution we have

$$\newcommand{\II}{\mathcal{I}} \newcommand{\dd}{\mathrm{d}} \mathcal{I} := \int_0^{2\pi} \frac{1}{5+ 3 \cos x} \, \dd x = \int_?^? \frac{1}{5+3(1-t^2)/(1+t^2)} \frac{2 \, \dd t}{1+t^2} = \int_?^? \frac{1}{t^2 + 4} \, \dd t$$

Question: what should these bounds be? I left them out for a reason.

Recall that $\tan(\pi/2)$ is undefined, since $\cos(\pi/2)=0$. So in reality, we actually have to handle two integrals here, by splitting the original at $x=\pi$. Then we get

$$\II = \int_0^\infty \frac{1}{t^2 + 4} \, \dd t + \int_{-\infty}^0 \frac{1}{t^2 + 4} \, \dd t = \int_{-\infty}^\infty \frac{1}{t^2 + 4} \, \dd t $$

Clearly, the antiderivative is

$$\frac 1 2 \arctan \frac t 2$$

(up to a constant). Taking $t \to \pm \infty$ will give $\pm \pi/4$, so the fundamental theorem returns $\pi/2$ as intended.

---

I think this overlooking of how the bounds change and where the substitution may be undefined is causing the issue here. You can't just get to that final integral and swap back to the $(0,2\pi)$ viewpoint: the substitution is, in some sense, stretching both the function in the integrand and the bounds as well, so the bounds have to switch with you whenever you swap the variables.

This is why, while in theory, you can just find an antiderivative and then apply the fundamental theorem with a back-substitution into your original variable to use its bounds, in practice it's usually better to keep track of the way the boundaries change along the way. Nuances like these get lost.

Another thing of note in this same vein: $t=\tan(x/2)$ sends $0$ and $2\pi$ to the same point, $0$. This is how you can see where you lost information: naively just changing the bounds (ultimately what you did) without considering the intermediate behavior just resulted in an integral of the type $\int_0^0 f(x) \, \dd x$, "obviously" "equal to" zero. However, the values in between those two points got sent, literally, across the entirety of the real line. And integration cares about those points too, after all.

In summary: be careful with how substitutions affect your bounds of integration, and the well-definedness of the substitution on the entire interval. It's not just the endpoints that matter!

Answer 2

Your first antiderivative is "correct", that isn't (quite) the problem.

When I say "correct" rather than correct, the point is that to speak accurately we should always talk about an antiderivative on a specific interval, see my answer here. And $$\frac{1}{2} \arctan \left(\frac{1}{2}\tan \frac{x}{2}\right)$$ cannot be the antiderivative of anything on the interval $[0,2\pi]$, because it is not defined when $x=\pi$.

One way to get around this is $$\eqalign{\int_0^{2\pi} \frac{1}{5+3 \cos x} dx &=\int_{-\pi}^\pi \frac{1}{5+3\cos x}\,dx\qquad\hbox{(integral over a full period)}\cr &=2\int_0^\pi \frac{1}{5+3\cos x}\,dx\qquad\hbox{(the integrand is even)}\cr &= \arctan \left(\frac{1}{2}\tan \frac{x}{2}\right)\bigg|_0^\pi\cr &=\frac\pi2\ .\cr}$$