I am trying to find the optimum solution for calculating and visualizing the critical point of an inverse power curve.
As an example, consider the curve of: $150x^{-0.4}$
I modeled the function using https://www.geogebra.org/graphing (type in $150x^-0.4$ as the function). A power curve is unlike a polynomial because it does not have a sudden vertex where the rate of change $=0$. Therefore I need to use a different method of calculating the maximum or minimum (depending on orientation) for the curve.
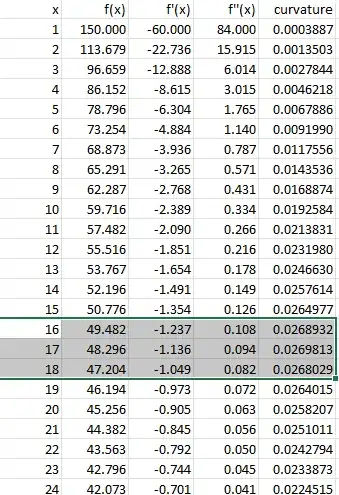
Visual inspection of this curve shows that maximum curvature in the 'elbow' is likely somewhere between $10<x<60$. I used recommendations for finding maximum curvature based on protocol provided in other forum threads:
The answer I calculated as the point of maximum curvature is (50.7, 31.2). However, I am not confident about this answer because I calculated curvature at each point and the answer is between 16 and 18 based on my calculation of curvature in excel. I don't know how to validate it though.
I have a couple inquiries:
- Is this the equation I should be using to find the apex or maximum of this curve?
- What is recommended software or programming that would aid in quantifying and visualizing this maximum curvature. It would be nice to have software like what is seen 52 seconds into this video: https://youtu.be/wyPXbvsd9nI?t=52 (other examples here, but none of them have been satisfying after a quick test. I'm still exploring)