integral $\int_0^a \frac{1}{\sqrt{1+x^6}} dx$ where $a=\frac{1}{\sqrt{\sqrt{3}-1}}$

Question

$I=\int_0^a \frac{1}{\sqrt{1+x^6}} dx$ where $a=\frac{1}{\sqrt{\sqrt{3}-1}}$ first, do binomial series on the integrand function, $\sum_{n=0}^\infty \binom{-\frac{1}{2}}{n}x^{6n}$ after integration, we got $\sum_{n=0}^\infty \frac{(-1)^n (\frac{1}{2})_n}{n!}\cdot\frac{a^{6n}}{6n+1}$ further, write $6n+1=\frac{(\frac{7}{6})_n}{(\frac{1}{6})_n}$, so the integral equals $\int_0^a \frac{1}{\sqrt{1+x^6}} dx=a\cdot F(\frac{1}{6},\frac{1}{2},\frac{7}{6};-a^6)$, where $F$ is hypergeometric function.

Questions:

Q1: the binomial series converges for $|x|<1$, but here $a>1$, can we do the binomial series expansion here?

Q2: how to proceed, the answer is $\frac{1}{8}B(\frac{1}{3},\frac{1}{6})$, where $B$ is beta function.

Answer 1

Some days before i have answered a question (4463639) involving similar expressions. There is also some link to Wolfram on the Incomplete Beta Function, and the following relations were displayed: $$ \begin{aligned} B(z;a,b) &= \int_0^z u^{a-1}(1-u)^{b-1}\; du \\ &= \frac 1az^a\; {}_2F_1(a,1-b;\ a+1;\ z) \\ &\qquad\qquad\qquad= z^a\sum_{n\ge 0}\frac{(1-b)_n}{n!\;(a+n)}\; z^n\qquad\text{if convergent} \ , \\ \text{ and also }& \\ B(z;a,b) &= \int_0^z u^{a-1}(1-u)^{b-1}\; du \\ &= \int_0^{z/(1-z)}\frac{v^{a-1}}{(1+v)^{a+b}}\;dv \end{aligned} $$ Notations slightly collide, for this reason i will use $$ w = (\sqrt 3-1)^{-1/2}\ , $$ and integrate on $[0,w]$.

---

(Q1) We are dealing with analytic functions, but we should avoid values for the (analitically extended) Gaussian hypergeometric function in the slit $(1, \infty)$, here is a link i found on this aspect: EM on hypergeometric functions.

(Q2) Let us compute the integral.

$$ \begin{aligned} 6\int_0^w\frac 1{(1+x^6)^{1/2}}\; dx &= 6\int_0^{w^6}\frac 1{(1+v)^{1/2}}\; \frac 16\; v^{-5/6}\; dv &&\text{ with } v = x^6 \\ &= \int_0^{w^6}\frac {v^{a-1}}{(1+v)^{a+b}}\; dv &&\text{ with } a=\frac 16\ ,\ b=\frac 13 \\ &= \int_0^{z/(1-z)}\frac {v^{a-1}}{(1+v)^{a+b}}\; dv&&\text{ with } z = \frac 19(3+2\sqrt 3) \\ % &= % B\left(z;a,b\right) % \\ &= B\left(z;\frac 16,\frac 13\right) \\ &= B\left(1;\frac 13,\frac 16\right) - \underbrace{B\left(1-z;\frac 13,\frac 16\right)} _{\color{red}{\text{Show it is }\frac 14B\left(\frac 13,\frac 16\right)\ !}} &&\text{ and let }Z = 1-z = \frac 29(3-\sqrt 3) \ . \end{aligned} $$ (Regarding (Q1) we can pass from $B(z,a,b)$ to an ${}_2F_1$-value for the argument $z$ with $z\approx 0.718233512793\in (0,1)$, also the last expression $B(1-z;b,a)$ has argument in $(0,1)$- so we have convergence if series are written. But we do not need this.)

Let us show the red marked equality: $$ \begin{aligned} B\left(1-z;\frac 13,\frac 16\right) &= B\left(Z;\frac 13,\frac 16\right) = \int_0^{V:=Z/(1-Z)}\frac{v^{1/3\ -\ 1}}{(1+v)^{1/3\ +\ 1/6}}\; dv \\[2mm] &\qquad\text{ and with $v=x^3$, $y=(1+v)^{1/2}$, } \\ &\qquad\text{ so that $y^2=1+v=1+x^3$, and $dv=3x^2\; dx$, and $v^{1/3\ -\ 1}=x^{-2}$} \\[2mm] &= 3\int _{(x,y)=(0,\ 1)} ^{(x,y)=\left(V^{1/3}\ ,\ (1+V)^{1/2}\right) =\left(\sqrt3-1\ ,\ \sqrt{6\sqrt 3-9}\right)} \ \frac{dx}y = 3\int_Q^P\frac{dx}y \\ &= 3\int_O^P\frac{dx}y - 3\int_O^Q\frac{dx}y \ , \end{aligned} $$ and the last integral is a path integral on $E(\Bbb R)$ where $E$ is the elliptic curve $y^2=x^3+1$. Let us use the notations $a=\sqrt 3$ and $b=\sqrt{6a-9}$

It turns out that the involved points $$ \begin{aligned} P &=(a-1\ ,\ b)=\left(\sqrt3-1\ ,\ \sqrt{6\sqrt 3-9}\right)\ ,\\ Q &=(0,1)\ , \end{aligned} $$ from $E(K)$ satisfy $4P=O=3Q$. Also $2P=(-1,0)$, and $2Q=-Q=(0,-1)$. Here is a piece of code giving this information in sage:

B = sqrt(6*sqrt(3) - 9)
K.<b> = NumberField( B.minpoly(), embedding=B.n() )
a = (b^2 + 9)/6
E = EllipticCurve(K, [0, 1])
P = E.point( (a - 1, b) )
P = E.point( (0    , 1) )
print(f'E = {E}')
print(f'The point P(a - 1, b) in E(K) has order {P.order()}.')
print(f'The point Q(    1, 0) in E(K) has order {Q.order()}.')

And we get (slightly manually rearranged to fit in the line):

E = Elliptic Curve defined by y^2 = x^3 + 1 over Number Field in b
    with defining polynomial x^4 + 18*x^2 - 27 with b = 1.179959679570986?
The point P(a - 1, b) in E(K) has order 4.
The point Q(    1, 0) in E(K) has order 3.

Because $dx/y$ is invariant w.r.t. the additive operation on $E$ we have: $$ \begin{aligned} \int_O^P\frac{dx}y &= \int_{P}^{2P}\frac{dx}y = \int_{2P}^{3P}\frac{dx}y = \int_{3P}^{O}\frac{dx}y \ , \\[2mm] \int_O^Q\frac{dx}y &= \int_Q^{2Q}\frac{dx}y = \int_{2Q}^O\frac{dx}y \ . \end{aligned} $$ Now use parametrizations of $E(\Bbb R)$ as follows. Let $x$ go from $\infty$ to $-1$, associate the path $\gamma_+(x)=(x, \ +\sqrt{1+x^3})\in E(\Bbb R)$, then let $x$ go from $-1$ to $+\infty$, and associate the path $\gamma_-(x)=(x, \ -\sqrt{1+x^3})\in E(\Bbb R)$. Let $\gamma$ be the full path, $\gamma =\gamma_+\cup\gamma_-$.

Let $J$ be the integral of $dx/y$ on $\gamma$, $J=-2\int_{-1}^\infty \frac{dx}{\sqrt{1+x^3}}$. Maybe it is best to have a picture, and to associate all integrals to fractions of an integral on the "whole contour $\gamma$ taken in trigonometric sense":

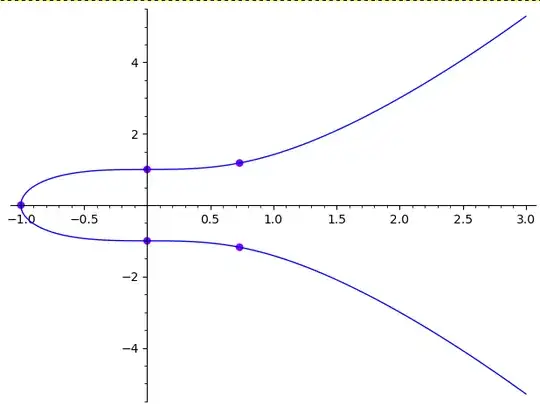
The two points on $Oy$ are $\pm Q$, the two points on the vertical $x=\sqrt3-1\approx 0.732$ are $\pm P$, the last marked point is $2P=(-1,0)$. We obtain $$ \begin{aligned} \int_{\sqrt 3-1}^\infty\frac{dx}{\sqrt{1+x^3}} &= \int_{\gamma_+\ ,\ x\in[\sqrt 3-1,\ \infty)}\frac{dx}{\sqrt{1+x^3}} = -\int_O^P\frac{dx}y = -\frac 14 J\ , \\ \int_{-1}^{\sqrt 3-1}\frac{dx}{\sqrt{1+x^3}} &= \int_{\gamma_+\ ,\ x\in[-1, \sqrt 3-1]}\frac{dx}{\sqrt{1+x^3}} = -\int_P^{2P}\frac{dx}y = -\frac 14J \ , \\ \int_0^\infty\frac{dx}{\sqrt{1+x^3}} &= \int_{\gamma_+\ ,\ x\in[0,\infty)}\frac{dx}{\sqrt{1+x^3}} = -\int_0^Q\frac{dx}y = -\frac 13 J\ , \\ 2\int_{-1}^0\frac{dx}{\sqrt{1+x^3}} &= \int_{\gamma_+\ ,\ x\in[-1,0]}\frac{dx}{\sqrt{1+x^3}} + \int_{\gamma_-\ ,\ x\in[-1,0]}\frac{dx}{\sqrt{1+x^3}} = -\int_Q^{2Q}\frac{dx}y = -\frac 13 J\ , \\ &\qquad\text{ and from here we can conclude} \\ \frac 13B\left(Z;\frac 13,\frac 16\right) &= \int_Q^P\frac {dx}y = \int_0^ {\sqrt3-1}\frac {dx}{\sqrt{1+x^3}} \\ &= \int_{-1}^ {\sqrt3-1}\frac {dx}{\sqrt{1+x^3}} - \int_{-1}^ 0\frac {dx}{\sqrt{1+x^3}} \\ &= -\frac 14J + \frac 16J = \left(\frac 14-\frac 16\right) \cdot 3 \int_0^\infty\frac {dx}{\sqrt{1+x^3}} = \frac 14 \int_0^\infty\frac {dx}{\sqrt{1+x^3}} \\ &= \frac 1{12} B\left(\frac 13,\frac 16\right) \end{aligned} $$

$\square$

Answer 2

This is based on hints from user pisco in comments to question, but it uses the theory of elliptic integrals as developed by Legendre (see details in this answer) instead of the more complicated theory of elliptic curves.

Let $\alpha=(\sqrt{3}-1)^{-1/2}$ and we need to compute the integral $$I=\int_0^\alpha \frac{dx}{\sqrt {1+x^6}}\tag{1}$$ Using substitution $x^2=t$ we get $$I=\frac{1}{2}\int_0^{\alpha ^2}\frac{dt}{\sqrt{t+t^4}}$$ Next we put $t=(1+x)/(2-x)$ so that $dt=3\,dx/(2-x)^2$ and $$t+t^4=\frac{(1+x)((2-x)^3+(1+x)^3)}{(2-x)^4}$$ and the right hand side simplifies to $$\frac{9(1+x^3)}{(2-x)^4}$$ so that $$I=\frac{1}{2}\int_{-1}^\beta\frac{dx} {\sqrt{1+x^3}}$$ where $$\beta=\frac{2\alpha^2-1}{\alpha^2+1}=\sqrt{3}-1$$ Putting $x=t^2-1$ we get $$I=\int_0^{\sqrt [4]{3}}\frac{dt}{\sqrt{3-3t^2+t^4}}\tag{2}$$ Legendre gives a general formula for integrals of above type $$Z=\int_0^x\left(\frac{f+gt^2}{\sqrt{a^2+2abt^2\cos\theta+b^2t^4}}-\frac{g}{b}\right)\,dt\tag{3}$$ as $$Z=\frac{bf+ag} {b\sqrt{ab}} F(\phi, k) - \frac{2ag}{b\sqrt{ab}}E(\phi,k)\tag{4}$$ where $k=\sin(\theta/2)$ and $$\cos^2\phi=\frac{\sqrt{a^2+2abx^2\cos\theta+b^2x^4}-(a\cos\theta+bx^2)}{2ak^2}\tag{5}$$ or equivalently $$x=\sqrt{\frac{a} {b}} \tan\phi\sqrt{1-k^2\sin^2\phi}\tag{6}$$ and $$F(\phi, k) =\int_0^{\phi}\frac{dx}{\sqrt{1-k^2\sin^2x}},E(\phi,k)=\int_0^{\phi}\sqrt{1-k^2\sin^2x}\,dx\tag{7}$$ are incomplete elliptic integrals of first and second kind respectively. The complete elliptic integrals are given as $$K(k) =F(\pi/2,k),E(k)=E(\pi/2,k)$$ Legendre uses the notation $$nF(\phi, k) =F(\phi_n, k) $$ where $n$ is a positive integer and says that $\sin\phi_n$ is an algebraic function of $\sin\phi$ which can be obtained using addition formulas for elliptic integrals. The formulas can be inverted in the sense that one can get $\sin\phi$ from $\sin\phi_n$ and Legendre handles special cases $n=2,3$ which we mention below.

Theorem 1 (Bisection formula): We have $$\sin\phi=\frac{\sin(\phi_2/2)}{\sqrt {\left(1+\sqrt{1-k^2\sin^2\phi_2}\right) /2} }$$ and if $\phi_2=\pi/2$ so that $2F(\phi,k)=K(k)$ then $$\sin\phi=\frac{1}{\sqrt{1+k'}},\cos\phi=\sqrt{\frac{k'}{1+k'}}$$ so that $$\tan\phi\sqrt{1-k^2\sin^2\phi}=1$$

Theorem 2 (Trisection formula): If $3F(\phi,k)=K(k)$ then $x=\sin\phi$ is a root of $$k^2x^4-2k^2x^3+2x-1=0$$ and in particular if $k=\cos(\pi/12)=k'_3$ then $\sin\phi=\sqrt{3}-1$.

Comparing integrals in $(2)$ and $(3)$ we see that $I=Z$ with $$a=\sqrt{3},b=1,f=1,g=0,\theta=5\pi/6$$ and hence we get $$k=\sin(\theta/2)=\cos(\pi/12)=k'_3$$ and further putting $x=\sqrt[4]{3}$ in $$x=\sqrt{\frac{a} {b}} \tan\phi\sqrt{1-k^2\sin^2\phi}$$ we get $$\tan\phi\sqrt{1-k^2\sin^2\phi}=1$$ and hence by theorem 1 we get $F(\phi, k) =K(k) /2$ and then using $(4)$ we have $$I=\frac{K(k'_3)}{2\sqrt[4]{3}}\tag{8}$$ Next we try to use another integral $$P=\int_0^1\frac{z^{-1/3}\,dz}{\sqrt{1-z^2}}\tag{9}$$ and relate it to $K(k'_3)$. Using the substitution $t=z^2$ we can note that $$P=\frac{1}{2}\int_0^1 t^{-2/3}(1-t)^{-1/2}\,dt=\frac{B(1/3,1/2)}{2}$$ so that $$P=\frac{\Gamma(1/3)\Gamma (1/2)}{2\Gamma(5/6)}\tag{10}$$ Again using substitution $z=(1-t^2)^{3/2}$ in $(9)$ we get $$P=\int_0^1\frac{3\,dt}{\sqrt{3-3t^2+t^4}}$$ and comparing this with $(3)$ we see that $P=Z$ with $$a=\sqrt{3},b=1,f=3,g=0,\theta=5\pi/6,x=1$$ so that $k=\cos(\pi/12)=k'_3$ and hence $$P=\frac{3}{\sqrt[4]{3}}F(\phi,k)$$ where $\cos^2\phi$ is obtained by putting $x=1$ in $(5)$. Doing the calculations we get $$\cos^2\phi=2\sqrt{3}-3$$ so that $\sin\phi=\sqrt {3}-1$ and using theorem 2 we see that $F(\phi, k) =K(k) /3$. And therefore we have $$P=\frac{K(k'_3)}{\sqrt[4]{3}}$$ Using equations $(8)$ and $(10)$ we finally get $$I=\frac{P} {2}=\frac{\Gamma(1/3)\Gamma (1/2)}{4\Gamma(5/6)} $$ as the value of integral in question.