Someone on social media (where I linked this post), Prof. Antoine Chambert-Loir, gave a solution. The outline below is from him; errors, if any, are mine.
The idea is to set
$$a_n = \operatorname{sl}^2(u_n) \tag{1}
$$
where $\operatorname{sl}$ is the lemniscate sine function.
Then the recurrence relation becomes
$$
\operatorname{sl}^2(u_{n+1}) = \frac{1-\sqrt{1-\operatorname{sl}^2(u_n)}}{1+\sqrt{1+\operatorname{sl}^2(u_n)}} = \operatorname{sl}^2(\tfrac{1}{2}u_{n}) \tag{2}
$$
using the bisection formulas and identities relating $\operatorname{sl}$ and $\operatorname{cl}$.
This shows that $u_{n+1} = \frac{1}{2}u_n$, and therefore
$$
u_n = \frac{2u_1}{2^{n}} \tag{3}
$$
But $a_1=1$ implies $\operatorname{sl}(u_1) =1$, which then gives
$$
u_1 = \int_0^1 \frac{dx}{\sqrt{1-x^4}} = \frac{\sqrt{\pi}\Gamma(5/4)}{\Gamma(3/4)} \tag{4}
$$
which finally leads to
$$
a_n = \operatorname{sl}^2(u_n) \operatorname*{\sim}_{n\to\infty} u_n^2 = \frac{4u_1^2}{4^n} = \frac{4\pi\Gamma(5/4)^2}{\Gamma(3/4)^2} \cdot 4^{-n} \tag{5}
$$
where $\varpi^2=\frac{4\pi\Gamma(5/4)^2}{\Gamma(3/4)^2}\approx 6.875185818$ ($\varpi$ being the lemniscate constant).
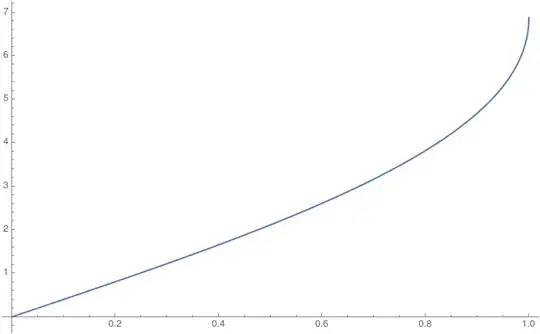
The above, as per the OP's question, corresponds to the initial condition $a_1=1$. Using the same argument, one easily gets that, for $a_1=\alpha\in[0,1]$, the limiting constant for $4^n a_n$ is given by
$$
C(\alpha) = 4\operatorname{arcsl}(\sqrt{\alpha})^2 = 4\left(\int_0^{\sqrt{\alpha}} \frac{dx}{\sqrt{1-x^4}}\right)^2 \tag{6}
$$
where $\operatorname{arcsl}$ is the lemniscate arcsine function.
The behavior of $C(\alpha)$ as $\alpha$ ranges from $0$ to $1$ is depicted below.