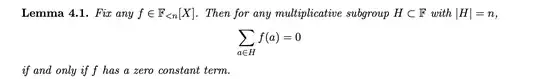Quoted from https://eprint.iacr.org/2019/601.pdf, but sadly with no proof.
-
1Please don't use pictures, use MathJax. Here is a tutorial. Did you already look into the reference [BCR+19]? – Dietrich Burde Mar 01 '22 at 10:14
-
what have you tried? To get started you should think about the case $f(x)=x$, i.e. the identity function. Can you prove that case? – Simon Mar 01 '22 at 10:24
-
Related. The case there is that $\Bbb{F}$ is finite, and $H$ is the entire multiplicative group. Nevertheless, the answers their work in this case as well. For it is well known that $H$ must be cyclic. – Jyrki Lahtonen Mar 01 '22 at 10:49
-
Anyway, calling this a duplicate of the one I linked to does not feel right. Therefore I won't use my dupehammer here. More so, because it would be immediately binding, and there are other problems with this question that need to be addressed, also. – Jyrki Lahtonen Mar 01 '22 at 10:50
1 Answers
It’s sufficient to prove it for $f=X^\alpha$, with $1\leq \alpha<n$.
Take $b\in H$. Observe that you can choose $f(b)=b^\alpha\neq 1$ because the polynomial $X^\alpha-1$ has a finite number of roots, that is at most $ \alpha<n=|H|$. You can say the same if $\alpha\not \equiv 0 \mod n$ because if $\alpha=kn+\beta$, with $1\leq \beta<n$, then there is $b\in H$ such that $b^\beta\neq 1$. Then $b^\alpha=b^\beta\neq 1$.
Set $S:= \sum_{a\in H}f(a)$. Then
$f(b)S=f(b)\sum_{a\in H} f(a)=\sum_{a\in H}f(ab)= S $
So that
$(f(b)-1)S=0$ and so $S=0$
This proof is related to the representation theory. In fact $f=X^\alpha\in H^*$, where $H^*$ is the group of characters with values in $\mathbb{F}$. Now there is the usual formula
$\sum_{a\in H} \phi(a)=0$ for each $\phi\in H^*\setminus{1}$
In your case $f=X^\alpha$ is different from $1$ if and only if $\alpha$ is not a multiple of $|H|=n$. Thus you can generalise your result taking $f\in \langle X^\alpha: \alpha\not \equiv 0 \mod n \rangle_\mathbb{F}$. Observe that $\langle X^\alpha: \alpha\not \equiv 0 \mod n \rangle_\mathbb{F}$ contains $\mathbb{F}_{ 1\leq \deg<n}[X]$.
- 10,123
-
2These are the key tricks. I do think that you need to explain why you can find $b\in H$ such that $b^\alpha\neq1$. In a multiplicative group $G$ of order $n=4$ it is perfectly possible that every element $b\in G$ satisfies $b^2=1$. Such a group $G$ cannot be a subgroup of the multiplicative group of a field because ... – Jyrki Lahtonen Mar 01 '22 at 10:53
-
@JyrkiLahtonen Thank you very much, Now I added something :) – Federico Fallucca Mar 01 '22 at 11:07
-
-
why $\sum_{\in}()=$? You mentioned
the group of characters, I didn't find the definition of that, do you meancharacter group? – omg Mar 01 '22 at 12:20 -
@omg because {ab: a\in H}=H and you are summing over H. The group of characters is the group of the morphisms group from $H$ to $\mathbb{F}^*$ – Federico Fallucca Mar 01 '22 at 13:07
-
-
@omg https://kconrad.math.uconn.edu/blurbs/grouptheory/charthy.pdf I wrote also some short notes but I can send you only by email. If you want, I can send you – Federico Fallucca Mar 01 '22 at 14:01
-