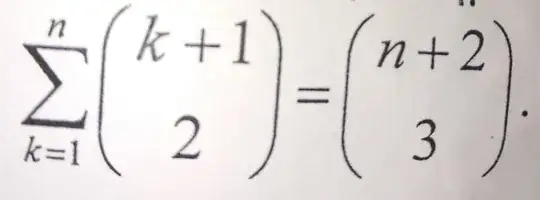mathimatic induction with SUM

Question

I want to do this with mathimatical induction,for every n>=1.

What I did : I know that basic step is for n=1 so

 ( 1+2    )and I have   (  3 )
 (    3   )             (  3 )

step 2 : let assume n=k is true

( n+2   )  it becomes        (  k + 2 ) 
(    3   )                   (     3  )

step 3: we have to prove that

( k+1   )   =      (  k + 2 ) 
(  2    )          (    3   )

we know that n=k+1 so

( k+1   )   =      (  k +1 + 2 ) 
 (  2    )          (    3   )

it gives us

( k+1   )   =      (  k + 3 ) 
 (  2    )          (    3   )

not sure if I go right or wrong.

Using $k$ both in the sum and your induction is sure to confuse you. Change one of those uses to $m$ instead. — Brian Moehring, Jan 24 '22 at 00:46

Brien Navarro · Accepted Answer · 2022-01-24T01:31:06.410

The induction is straightforward and follows from Pascal's rule

Base case

The case $n=1$ is trivial (you made the calculation in you question).

Inductive hypothesis

Suppose that the proposition is true for $n$. This means that we assume that the following is true:

$$\sum_{k=1}^{n} {k+1\choose 2 }={n+2 \choose 3}$$

Inductive step (Prove that the proposition is true for n+1)

Consider the sum $$\sum_{k=1}^{n+1} {k+1\choose 2 }=\sum_{k=1}^{n} {k+1\choose 2 }+ {n+2 \choose 2}$$

Since by inductive hypothesis the assertion is true for $n$ we apply the hypothesis for calculate the sum.

Hence $$\sum_{k=1}^{n+1} {k+1\choose 2 }= {n+2\choose 3 }+ {n+2 \choose 2}={n+3 \choose 3}$$

And this complete the induction. Therefore the assertion is true for all $n\geq 1$.

Remark

Notice that the least step is possibly since we apply the pascal`s rule to the sum of the two binomial coefficients.

1 Answers1