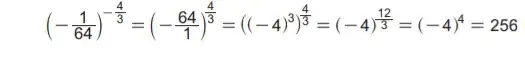I have included this picture in its original form from my textbook here.
I think this is wrong because it contradicts the definition of $a^x$.
Because we define
$$a^x=e^{x\ln a}$$
where $a>0,x\in\mathbb R$.
Am I making a mistake or is the textbook wrong?