Rigid nonagons and rational solutions of a hyperelliptic equation

Question

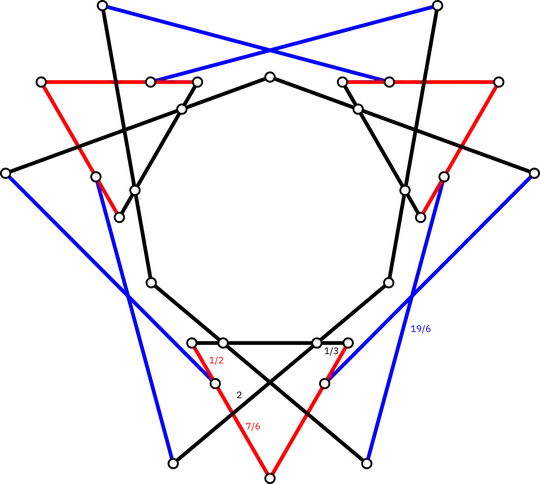
Here is a rational bracing of the regular nonagon of side $1$ with $12$ extra rods (extensions of the nonagon sides don't count), fulfilling a long-held dream of mine:

I found it in a similar manner to the rationally braced pentagon by considering the following framework where $a,b,c$ and the blue edge length are all rational – rods are interpreted as vectors pointing from bottom to top:

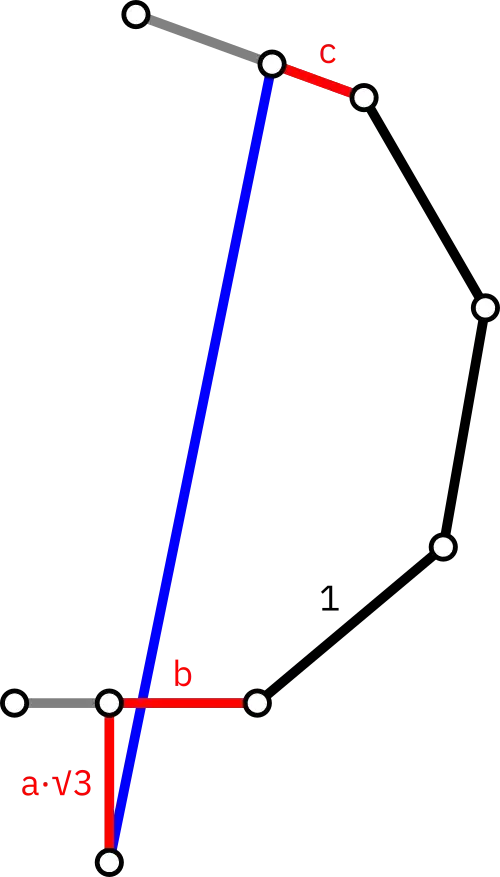
$a,b,c>0$ as depicted, while the bottom-most point can be fixed relative to the horizontal rod by building an equilateral triangle on it, so there's no problem in making the first vector length $a\sqrt3$. Then the blue rod as a complex number is $$a(z^3-z^6)+b+z+z^2+z^3+cz^4$$ where $z=e^{2i\pi/9}$, and its squared length is in $\mathbb Q(z)$: $$3a^2+b^2+c^2+3a-b-c+3+(1+2ac)z-(1+2ac)z^2+(-1-3a-b-c+ac+bc)z^4+(-2-3a-b-c-ac+bc)z^5$$ Since $\{1,z,z^2,z^3,z^4,z^5\}$ is a $\mathbb Q$-basis for $\mathbb Q(z)$ yet the expression has to be a rational square, the coefficients of $z$ to $z^5$ must be zero, leading to $b$ and $c$ expressed in terms of $a$: $$b=\frac{1-3a-6a^2}{1+2a}\qquad c=-\frac1{2a}$$ Substituting gives the blue rod length as $$\frac{\sqrt{1+6a+24a^2+48a^3+144a^4+288a^5+192a^6}}{2a(1+2a)}$$ so all rational bracings under this framework correspond to rational points on the hyperelliptic curve $y^2=1+6a+24a^2+48a^3+144a^4+288a^5+192a^6$.

Using PARI/GP I have found four pairs of rational points on the curve with $a=-\frac12,0,\frac14,\frac32$. The first two values cause a divide-by-zero upon substituting, the third gives the bracing shown at top and the last gives a vertex-edge-degenerate and very large but still rigid bracing. The question here, since this is a hyperelliptic curve, is natural:

Does $a\in\left\{-\frac12,0,\frac14,\frac32\right\}$ describe the complete set of rational points on $y^2=1+6a+24a^2+48a^3+144a^4+288a^5+192a^6$?

I suspect the problem can be resolved with current methods – although the rank of the Mordell–Weil group of the Jacobian is $2$, the sextic in $a$ is also a defining polynomial for $\mathbb Q(z)$, which means it has Galois group $C_6$ and (I think) "elliptic curve Chabauty" as mentioned in this MathOverflow answer (and explicated for $y^2=x^6+x^2+1$ here, though I can't follow the whole thing) can be applied.

It may help that the substitution $a=\frac1{2(t-1)}$ produces a "minimal" birationally equivalent curve $$y^2=t^6-3t^5+6t^4-8t^3+12t^2-6t+1$$

Answer 1

I sent an email to Michael Stoll himself with this problem, and he gave me a Magma program proving that the rational points I found are all there are. The calculations easily fit into the allowed running time on the Magma Calculator; an annotated version follows.

P<x> := PolynomialRing(Rationals());
f := x^6 - 3*x^5 + 6*x^4 - 8*x^3 + 12*x^2 - 6*x + 1;
C := HyperellipticCurve(f);
J := Jacobian(C);
// verify the claim on the MW group
time MW, mMW, flag1, flag2 := MordellWeilGroup(J);
assert flag1 and flag2 and Invariants(MW) eq [0,0]; // Z^2

We first compute the $2$-Selmer set of the curve with TwoCoverDescent; for elliptic curve Chabauty (ECC) to work the mapping from rational points to this set, where the mapping returned by the function is used, must be surjective. The rational points on the minimal model have $x$-coordinates $(0,4/3,3,\infty)$ and a suitable cover is $(0,3,\infty)$:

time SelC, mSelC := TwoCoverDescent(C);
ptsC := Points(C : Bound := 1000);
xptsC := [0, 3]; assert Set(xptsC) subset {pt[1]/pt[3] : pt in ptsC | pt[3] ne 0};
assert not IsEmpty(PointsAtInfinity(C));
assert #SelC eq 3
         and SelC eq {Universe(SelC)!0} // points at infinity map to 0
                       join {mSelC(xi - Domain(mSelC).1) : xi in xptsC};

Now we factor the sextic into three quadratics over $\mathbb Q(\zeta_9^+)$ (defined by $x^3-3x+1)$ and pick any two factors to form a quartic $h$. The elliptic curves needed for ECC are then $y^2=h(t)h(x)$ where $t$ is an $x$-coordinate in the cover; for general hyperelliptic curves we would require $\deg(h)$ or $\deg(p/h)$, where $y^2=p(x)$, to be even:

K := NumberField(x^3 - 3*x + 1);
factfK := [e[1] : e in Factorization(ChangeRing(f, K))];
// Take product of first two factors to define genus 1 quotients
// of the double cover of C associated to the factorization.
// (It doesn't matter which two factors we take, since the
// products are all Galois conjugate.)
h := factfK[1]*factfK[2];
Hyps := [HyperellipticCurve(d*h) : d in [1] cat [Evaluate(h, xi) : xi in xptsC]];
xptsCi := [Infinity()] cat xptsC;
Ells := [<E, HtoE> where E, HtoE := EllipticCurve(Hyps[i], Rep(Points(Hyps[i], xptsCi[i])))
          : i in [1..#Hyps]];
// Find minimal models (possible, since K has class number 1)
// to facilitate the Mordell-Weil group computation.
Emins := [<Emin, EtoEmin> where Emin, EtoEmin := MinimalModel(e[1]) : e in Ells];

For ECC to work the Mordell–Weil ranks of all these elliptic curves over the defined number field must be strictly less than the degree of the extension, here $3$. It turns out here that they all have rank $2$, so we are all set:

time MWs := [<MW, MWtoE, fl1 and fl2> where MW, MWtoE, fl1, fl2 := MordellWeilGroup(e[1])
              : e in Emins];
assert forall{e : e in MWs | e[3] and Invariants(e[1]) eq [2, 2, 0, 0]}; // all Z/2 + Z/2 + Z^2

Finally we apply ECC proper using more Magma functions. Many of the critical functions for this computation were in fact coded by Stoll and Nils Bruin:

P1 := ProjectiveSpace(Rationals(), 1);
Ecovs := [Expand(Inverse(Emins[i,2])*Inverse(Ells[i,2])*map<Hyps[i] -> P1 | [Hyps[i].1, Hyps[i].3]>)
            : i in [1..#Hyps]];
MWmaps := [map<MWs[i,1] -> Emins[i,1] | m :-> MWs[i,2](m)> : i in [1..#Hyps]];
function ECChab(MWmap, Ecov)
  time inMW := Chabauty(MWmap, Ecov);
  xcoords := {Ecov(MWmap(m)) : m in inMW};
  return &join[xi[2] eq 0 select PointsAtInfinity(C) else Points(C, xi[1]/xi[2])
           : xi in xcoords];
end function;
allpoints := &join[ECChab(MWmaps[i], Ecovs[i]) : i in [1..#Hyps]];

allpoints now provably contains all rational points on the curve, and this list corresponds one-to-one with the list I had when I asked this question, so there are indeed only two nonagon bracings of the above type. The full code I was sent, together with Stoll's own comments, can be found here.