Closed form of $\int e^{i\csc^2(x)}dx=\int \cos\left(\csc^2(x)\right)dx+i\int \sin\left(\csc^2(x)\right)dx$

Question

This will be an experimental integral with the final result using the Kampé de Fériet function with the goal integrals being: $$\int \cos\left(\csc^2(x)\right)dx,\int\sin\left(\csc^2(x)\right)dx\implies \int e^{ i\csc^2(x)}dx=\int\cos\left(\csc^2(x)\right)+i\sin\left(\csc^2(x) \right)dx $$ which already is related to

Area under period of $$a^{\csc(x)}$$

Here is the method that will be used with term by term integration and a Gauss Hypergeometric function with 2 constant arguments: $$\int e^{i\csc^2(x)}dx=\int \sum_{n=0}^\infty \frac{i^n \csc^{2n}(x)}{n!}dx=\sum_{n=0}^\infty\frac{i^n}{n!}\int\csc^{2n}(x)dx=C-\sum_{n=0}^\infty \frac{i^n}{n!}\cos(x)\sin^2(x)^{n+\frac12}\csc^{2n+1}(x)\,_2\text F_1\left(\frac12,n+\frac12,\frac32,\cos^2(x) \right)$$ Next let’s expand the hypergeometric function as seen in the corresponding bolded link using the Pochhammer Symbol function. Let’s also switch the indices so that we can use the Kampé de Fériet bolded link’s formula more easily:

$$C-\sum_{m=0}^\infty \frac{i^m}{m!}\cos(x)\sin^2(x)^{m+\frac12}\csc^{2m+1}(x)\,_2\text F_1\left(\frac12,m+\frac12,\frac32,\cos^2(x) \right)=C-\cos(x)\sum_{m=0}^\infty \frac{i^m}{m!}\sin^2(x)^{m+\frac12}\csc^{2m+1}(x)\sum_{n=0}^\infty\frac{\left(\frac12\right)_n\left(m+\frac12\right)_n \cos^{2n}(x)}{\left(\frac32\right)_nn!}= C-\cos(x)\sum_{m=0}^\infty \frac{i^m}{m!}\sin^2(x)^{m+\frac12}\csc^{2m+1}(x)\sum_{n=0}^\infty\frac{\left(m+\frac12\right)_n \cos^{2n}(x)}{(2n+1)n!}$$

Now let’s combine sums and leave the Pochhammer Symbols alone until later steps. Let’s not “simplify” because this would constrict the domain:

$$C-\cos(x)\sum_{m=0}^\infty\sum_{n=0}^\infty \frac{i^m}{m!}\sin^2(x)^{m+\frac12}\csc^{2m+1}(x)\frac{\left(\frac12\right)_n\left(m+\frac12\right)_n \cos^{2n}(x)}{\left(\frac32\right)_nn!}= C-\sqrt{\sin^2(x)}\cot(x)\sum_{m=0}^\infty\sum_{n=0}^\infty\frac{\left(\frac12\right)_n\left(m+\frac12\right)_n (i\csc^2(x)\sin^2(x))^m\cos^{2n}(x)}{\left(\frac32\right)_nm!n!} $$

There is a problem as the $\left(m+\frac12\right)_n$ cannot use the Kampé de Fériet function, so we need to do the following:

$$\left(m+\frac12\right)_n =\frac{\Gamma\left(m+n+\frac12\right)}{\Gamma\left(m+\frac12\right)}= \frac{\Gamma\left(m+n+\frac12\right)}{\Gamma\left(m+\frac12\right)} \frac{\Gamma\left(\frac12\right)}{\Gamma\left(\frac12\right)}=\frac{\left(\frac12\right)_{m+n}}{\left(\frac12\right)_m}$$

Therefore:

$$ C-\sqrt{\sin^2(x)}\cot(x)\sum_{m=0}^\infty\sum_{n=0}^\infty\frac{\left(\frac12\right)_n\left(m+\frac12\right)_n (i\csc^2(x)\sin^2(x))^m\cos^{2n}(x)}{\left(\frac32\right)_nm!n!}= C-\sqrt{\sin^2(x)}\cot(x)\sum_{m=0}^\infty\sum_{n=0}^\infty\frac{\left(\frac12\right)_{m+n}\left(\frac12\right)_n(i\csc^2(x)\sin^2(x))^m\cos^{2n}(x)}{\left(\frac12\right)_m\left(\frac32\right)_nm!n!} $$

When the Kampé de Fériet function is defined as:

$$\text F^{p,r,u}_{q,s,v}\left(^{a_1,…,a_p;c_1,…,c_r;f_1,…,f_u}_{b_1,…,b_q;d_1,…,d_s;g_1,…,g_v}\ x,y\right)\mathop=^\text{def}\sum_{m=0}^\infty\sum_{n=0}^\infty\frac{\prod\limits_{j=1}^p(a_j)_{m+n} \prod\limits_{j=1}^r(c_j)_m \prod\limits_{j=1}^u (f_j)_n x^my^n}{\prod\limits_{j=1}^q (b_j)_{m+n} \prod\limits_{j=1}^s(d_j)_m \prod\limits_{j=1}^v(g_j)_n m!n!}$$

Therefore:

$$\int e^{ i\csc^2(x)}dx=C-\sqrt{\sin^2(x)}\cot(x)\sum_{m=0}^\infty\sum_{n=0}^\infty\frac{\left(\frac12\right)_{m+n}\left(\frac12\right)_n(i\csc^2(x)\sin^2(x))^m\cos^{2n}(x)}{\left(\frac12\right)_m\left(\frac32\right)_nm!n!}= C-\sqrt{\sin^2(x)}\cot(x)\text F^{1,0,1}_{0,1,1}\left(^{\frac12;;\frac12}_{;\frac12;\frac32}\ i\csc^2(x)\sin^2(x),\cos^2(x)\right) $$

which is a closed form in terms of a fairly common hypergeometric function and sign function. The problem is that this function only has $p,q,r,s,u,v$ values of $0,1$, so we can probably simplify the Kampé de Fériet function in terms of simpler functions like how with the following Normalized Fresnel Integral functions:

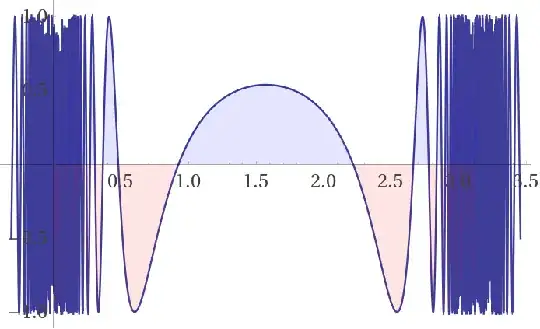
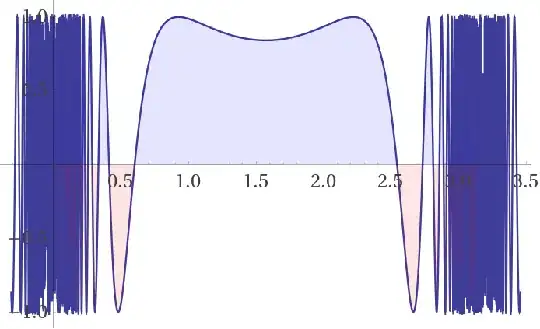
$$\int_0^\pi \cos(\csc^2(x))dx=\pi\left(1-\text C\left(\sqrt{\frac2\pi}\right)- \text S\left(\sqrt{\frac2\pi}\right)\right)=0.09655932…:$$

or

$$\int_0^\pi \sin(\csc^2(x))dx=\pi\left(\text C\left(\sqrt{\frac2\pi}\right)- \text S\left(\sqrt{\frac2\pi}\right)\right)=1.48957873…:$$

which can also be written in terms of Error functions. So how can we write

$$\int e^{i\csc^2(x)}dx=\int \cos\left(\csc^2(x) \right)dx+i\int \sin\left(\csc^2(x) \right)dx= C-\sqrt{\sin^2(x)}\cot(x)\text F^{1,0,1}_{0,1,1}\left(^{\frac12;;\frac12}_{;\frac12;\frac32}\ i\csc^2(x)\sin^2(x),\cos^2(x)\right)\mathop=^{0\ne x\in\Bbb R} C-\text{sgn}(\sin(x))\cos(x)\text F^{1,0,1}_{0,1,1}\left(^{\frac12;-;\frac12}_{-;\frac12;\frac32}\ i,\cos^2(x)\right) $$

in another closed form via less general functions? A solution verification is also requested. Please correct me and give me feedback!

Answer 1

The Owen T function is used for statistics, but has applications like the following definition:

$$2\pi \cdot\text T(x,a)\mathop=^\text{def} \int_0^a\frac{e^{-\frac{x^2}2\left(t^2+1\right)}}{t^2+1}dt$$

We can easily use a series expansion for the exponential function with index $n$, but that would case a hypergeometric function with a negative argument index of $-n$ which cannot really be converted into $n$ in the function. This problem is due to the positive exponent in the $e^y$, it is better to do the following substitution to shape make it easier to turn into a Kampé de Feriét function. We just need an identity, so keep in mind possible restrictions:

$$\int_0^a\frac{e^{-x^2\left(t^2+1\right)}}{t^2+1}dt\ \mathop=^{t^2+1=\frac1{u^2+1}\implies t=\pm \sqrt{\frac1{u^2+1}-1}}_{dt=\frac i{(u^2+1)^\frac32}du,u>0}\ i\int_0^{\sqrt{-\frac{a^2}{a^2+1}}} (u^2+1)\frac{e^{-\frac{x^2}{u^2+1}}}{(u^2+1)^\frac32}du=i\int_0^{\sqrt{-\frac{a^2}{a^2+1}}} \frac{e^{-\frac{x^2}{u^2+1}}}{(u^2+1)^\frac12}du=i\int_0^{\sqrt{-\frac{a^2}{a^2+1}}} \sum_{m=0}^\infty\frac{(-1)^mx^{2m}}{m!(u^2+1)^m(u^2+1)^\frac12}du=i \sum_{m=0}^\infty\frac{(-1)^mx^{2m}}{m!}\int_0^{b} (u^2+1)^{-m-\frac12}du$$

The upper bound will be called $b$ by definition. Let there be an integration using a Gauss hypergeometric series and Pochhammer symbol:

$$i \sum_{m=0}^\infty\frac{(-1)^mx^{2m}}{m!}\int_0^b (u^2+1)^{-m-\frac12}du=i \sum_{m=0}^\infty\frac{(-1)^mx^{2m}}{m!}b\sum_{n=0}^\infty \frac{\left(\frac12\right)_n \left(m+\frac12\right)_n(-b^2)^n}{\left(\frac32\right)_n n!}$$

Notice the similar coefficients to the original problem. We can change the pochhammer symbol by:

$$\left(m+\frac12\right)_n =\frac{\Gamma\left(m+n+\frac12\right)\Gamma\left(\frac12\right)}{\Gamma\left(m+\frac12\right)\Gamma\left(\frac12\right)}=\frac{\left(\frac12\right)_{m+n}}{\left(\frac12\right)_m}$$

Therefore we can use the question’s Kampé de Feriét function link:

$$i \sum_{m=0}^\infty\frac{(-1)^mx^{2m}}{m!}b\sum_{n=0}^\infty \frac{\left(\frac12\right)_n \left(m+\frac12\right)_n(-b^2)^n}{\left(\frac32\right)_n n!}=ib \sum_{m=0}^\infty\sum_{n=0}^\infty \frac{\left(\frac12\right)_{m+n}\left(\frac12\right)_n \left(-x^2\right)^m\left(-b^2\right)^n}{\left(\frac12\right)_m\left(\frac32\right)_n m!n!}=i b\,\text F^{1,0,1}_{0,1,1}\left(^{\frac12;;\frac12}_{;\frac12;\frac32}\ -x^2,-b^2\right)$$

which we now need to form into:

$$\int e^{i\csc^2(x)}dx=\int \cos\left(\csc^2(x) \right)dx+i\int \sin\left(\csc^2(x) \right)dx= C-\sqrt{\sin^2(x)}\cot(x)\text F^{1,0,1}_{0,1,1}\left(^{\frac12;;\frac12}_{;\frac12;\frac32}\ i\csc^2(x)\sin^2(x),\cos^2(x)\right)=$$

To finish the answer, let’s calculate $b$:

$$b={\sqrt{-\frac{a^2}{a^2+1}}}\implies -b^2=\frac{a^2}{a^2+1}$$

Therefore:

$$\text T(x,a)=-\frac{{\sqrt{\frac{a^2}{a^2+1}}}}{2\pi}\,\text F^{1,0,1}_{0,1,1}\left(^{\frac12;;\frac12}_{;\frac12;\frac32}\ -x^2,\frac{a^2}{a^2+1}\right)$$

Solving for $a,x$ and taking the positive square root branch gives the final answer as:

$$\int e^{i\csc^2(x)}dx=\int \cos\left(\csc^2(x) \right)dx+i\int \sin\left(\csc^2(x) \right)dx= -2\pi \sqrt{\cot^2(x)}\tan(x)\text T\left(1-i,\sqrt{\cot^2(x)}\right)+C\mathop=^{x\in\Bbb R} -2\pi\text{sgn}(\cot(x))\text T\left(1-i,|\cot(x)|\right)+C$$

Here is proof of the result with this computation

Therefore one special case is with the Imaginary Error function and Fresnel Integrals:

$$\int_0^\frac\pi4 e^{i\csc^2(x)}dx= \int_0^\frac\pi2 e^{i\csc^2(x)}dx -\int_\frac\pi4^\frac\pi2 e^{i\csc^2(x)}dx =\int_0^1 \frac{e^{i(x^2+1)}}{x^2+1}dx=2\pi(\text T(1-i,\infty)-\text T(1-i,1))=\frac\pi2+\frac\pi2\left((i-1)\text C\left(\sqrt{\frac2\pi}\right)-(1+i) \text S\left(\sqrt{\frac2\pi}\right)\right)+\frac\pi 4\left(\text{erfi}^2\left(\sqrt[4]{-1}\right)+1\right) $$

Note that the following code also applies with the Complementery Error function:

π/2 + 1/2 ((-1 + i) π C(sqrt(2/π)) - (1 + i) π S(sqrt(2/π))) = π/2 + 1/2 (-(1 + i) π (1/2 + 1/4 (1 + i) (i erfc(1/2 (1 - i) sqrt(π) sqrt(2/π)) - erfc(1/2 (1 + i) sqrt(π) sqrt(2/π)))) + (-1 + i) π (1/2 - 1/4 (1 - i) (i erfc(1/2 (1 - i) sqrt(π) sqrt(2/π)) + erfc(1/2 (1 + i) sqrt(π) sqrt(2/π)))))

Here is a plot of the real, cosine, part:

Here is a plot of the imaginary, sine, part:

Please correct me and give me feedback!

It is hard to separate real and imaginary parts of the OwenT function unless you use Complex Components