3

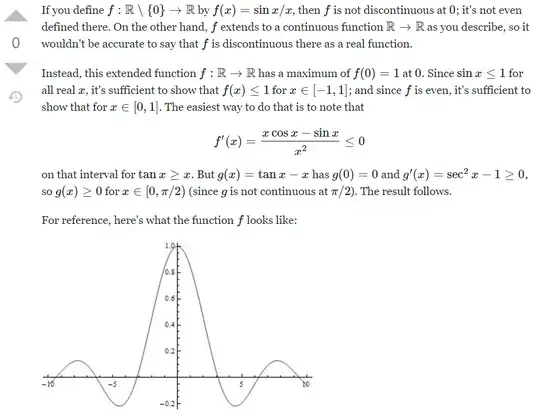
This question is based on this post. Here is the question:

At $x=0$ , $\frac{\sin x}{x}$ has ____? (Options are maxima, minima, point of inflection, dicontinuity)

I have failed to draw a plausible conclusion from what the answers say and the chat discussion(very interesting) there.

Here are some of the points that I wish to clarify:

1) Is it relevant to talk about continuity at a point where a function isn't even defined(first, third answers ( * , *** ))?

2) How can one extend the domain of the function to remove this discontinuity

3) The original question does not talk about extending the domain of the function, so is answer 2 ( ** ) valid?

Pictures of answers for reference:

(*)enter image description here

( ** )enter image description here

( *** )enter image description here

DatBoi
  • 4,097

2 Answers2

3

The question is not well posed since the function is not defined at $x=0$ and therefore it is meaningless ask for continuity for a point out of its natural domain.

If we define $f(0)=0$ then the new function has a removable discontinuity since we can redefine $f(0)=1$ and this final new function has a maximum at that point.

Refer also to the related

user
  • 162,563
  • Agreed, the question has been phrased poorly. Just to be clear, the function has a removable discontinuity now that the condition $f(0)=0$ is added right?(and not previously) – DatBoi Sep 27 '21 at 17:03
  • @DatBoi Yes, otherwise it is continuous. – user Sep 27 '21 at 17:09
1

To answer your second question, we can extend $f(x) = \frac{\sin{x}}{x}$ to a continuous function by defining $$\bar{f}(x) = \begin{cases} f(x), &x\ne 0\\ 1, &x=0 \end{cases}.$$ We often call $\bar{f}$ the continuous extension of $f$ to $\mathbb{R}$. Here, then, we have that $\bar{f}$ is defined on all of $\mathbb{R}$, so one only needs show that $\bar{f}$ is also continuous at $x = 0$.

DMcMor
  • 10,059