2

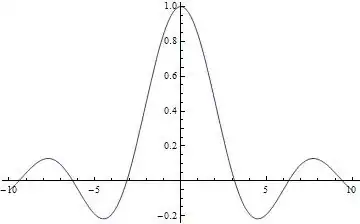
At $x=0$ , $\frac{\sin x}{x}$ has ____? (Options are maxima, minima, point of inflection, dicontinuity)

I am aware of the fact that $\lim_{x \to 0} \frac{\sin x}{x}$ approaches to $1$.

First I checked for first derivative :

$$\frac{x \cos x - \sin x}{x^{2}} = 0$$

$$\implies x \cos x = \sin x$$

$$\implies x = \tan x$$

$$\implies x = 0$$

$\therefore$ there is a point of inflection at $x = 0$

It's obviously not point of minima because, the value is tending to 1.

It's not maxima because $\frac{\sin x}{x}$ can exceed 1 as $x$ in denominator will be less than 1 $\therefore$ the value of fraction may exceed 1 at some point.

$\therefore$ it should be point of inflection. Am I correct ?

Michael Hardy
  • 1
Mojo Jojo
  • 481

3 Answers3

1

The correct answer is discontinuity. Whenever we have division by $0,$ there is a discontinuity. Although the limit at $x = 0$ does exist (it equals $1$), there is still a discontinuity. None of the other choices are correct.

K. Jiang
  • 10,436
  • 5
    How can a function have a discontinuity at a point where it is not even defined? It's like saying the function $h:\mathbb N \to \mathbb R$ given by $h(n)=n$ has a discontinuity at $n=\pi$. – TonyK Mar 05 '16 at 20:16
  • 1
    Is the function $f(x) = x^2/x$ discontinuous at $x = 0$? – anomaly Mar 05 '16 at 20:24
  • 1
    @anomaly: no, it is undefined at $x=0$. – TonyK Mar 05 '16 at 20:42
0

If you define $f:\mathbb{R}\setminus \{0\} \to \mathbb{R}$ by $f(x) = \sin x/x$, then $f$ is not discontinuous at $0$; it's not even defined there. On the other hand, $f$ extends to a continuous function $\mathbb{R} \to \mathbb{R}$ as you describe, so it wouldn't be accurate to say that $f$ is discontinuous there as a real function.

Instead, this extended function $f:\mathbb{R} \to \mathbb{R}$ has a maximum of $f(0) = 1$ at $0$. Since $\sin x \leq 1$ for all real $x$, it's sufficient to show that $f(x) \leq 1$ for $x\in [-1, 1]$; and since $f$ is even, it's sufficient to show that for $x\in [0, 1]$. The easiest way to do that is to note that \begin{align*} f'(x) = \frac{x \cos x - \sin x}{x^2} \leq 0 \end{align*} on that interval for $\tan x \geq x$. But $g(x) = \tan x - x$ has $g(0) = 0$ and $g'(x) = \sec^2 x - 1\geq 0$, so $g(x) \geq 0$ for $x\in [0, \pi/2)$ (since $g$ is not continuous at $\pi/2$). The result follows.

For reference, here's what the function $f$ looks like:

enter image description here

anomaly
  • 26,475
0

A $x=0$, the function $\dfrac{\sin x} x$ has a removable discontinuity, and once the discontinuity is removed, it has a global maximum at that point.

You can see that by observing that $\sin x<x$ for $x>0$ and $\sin x > x$ for $x<0$, so $\dfrac{\sin x} x < 1$ for $x\ne 0$, and the limit at $0$ is $1$.

Michael Hardy
  • 1