0

A K-input lookup table (K-LUT) can represent any function with K boolean inputs and a single boolean output. The number of possible functions represented by this LUT is $2^{2^K}$ according to this previous question, and other online resources.

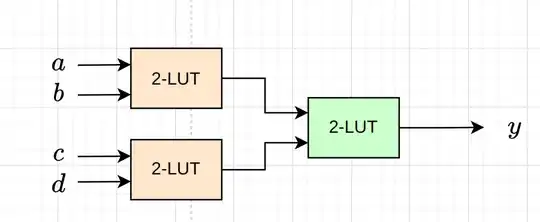
I am interested in finding the number of possible functions represented by a directed acyclic graph of LUTs. A simple example is shown below:

simple network of 2-LUTs

I am also interested in more complicated DAGs with non-uniform LUT sizes and more interesting connectivities of the input. For example, when one input is connected more than once, or when an input is connected to deeper levels of the DAG. Also, I am interested in DAGs with multiple outputs as well.

This feels like it is a solved problem but I can't find anything that computes the number of possible functions that are described by these structures.

mohsaied
  • 59

1 Answers1

1

For your three-node example, a brute force calculation says that you can represent $520$ different boolean functions on the four input bits. This is small fraction of all $2^{2^4}=65536$ boolean functions on four bits. By googling around with this 520 and words like "boolean function", one finds something.

In Thomas Fink's paper Composition of Boolean functions restricts biologically permitted logics (submitted to Physical Review Letters, 2021), Table 1 lists the numbers of boolean functions realizable by composing smaller functions in a particular way; your example corresponds to "composition structure 2,2" and has value 520. The table goes up to "3,3,3" which has three 3-input functions, whose outputs go to a fourth 3-input function, so the composition is a boolean function on 9 bits. The table says there are $447\,032\,128$ such functions.

Another finding is Farhoodi, Roozbeh; Filom, Khashayar; Jones, Ilenna Simone; Kording, Konrad Paul, On functions computed on trees, ZBL07164909. Their Corollary 1 says that the number of boolean functions on $n$ bits, realizable as binary trees (if I understand correctly this means composition of 2-input operations) has the surprisingly simple expression $(2 \cdot 6^n + 8)/5$. Plugging in $n=1,2,3,4,5$ to this formula one obtains $4,16,88,520,3112$, which is also OEIS A005618.

These are just some pointers, but starting a literature search with something is usually easier than starting it with nothing.

A more general treatment of this topic, the complexity of boolean functions as implemented by circuits, is Jukna's book Boolean Function Complexity (Springer 2012).

Jukka Kohonen
  • 2,784