I have a question about t.b.'s answer in How to define Homology Functor in an arbitrary Abelian Category?. I will make my question self-contained by rewriting some part of that answer.
Fix an abelian category. Given a chain complex
\begin{equation}
\operatorname{Ob} \overset{f}{\longrightarrow} \operatorname{Ob} \overset{g}{\longrightarrow} \operatorname{Ob}
\end{equation}
one can associate the following morphisms.
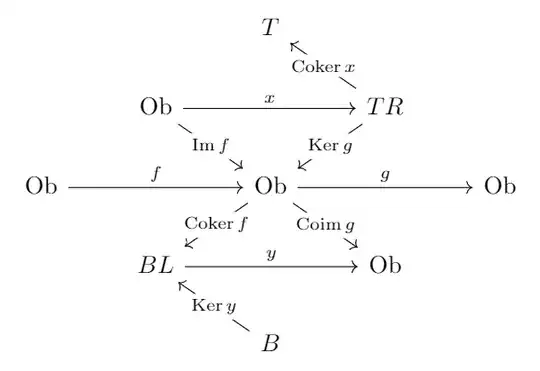
Here $\operatorname{Ob}$ stands for "object" (without name), $T$ for "top", $TR$ for "top right" etc. And $x$ and $y$ are the unique morphisms making the diagram commute. The above answer says that the homology of the chain complex can be defined in three ways:
- $\operatorname{Coker}x$
- $\operatorname{Ker}y$
- $\operatorname{Im}(\operatorname{Coker}f\circ\operatorname{Ker}g)$.
Why are these definitions the same? I somehow managed to prove that there are unique morphisms $T\to BL$ and $TR\to B$ such that $TR\to T\to BL = TR\to B\to BL = \operatorname{Coker}f\circ\operatorname{Ker}g$. Now if I show that $T\to BL$ is monic and that $TR\to B$ is epic, then I can use the following theorem from Peter Freyd's "Abelian Category," and I will be done.
"Unique factorization theorem" for abelian categories, 2.19 If $A\to B=A\to I\to B$ where $A\to I$ is epimorphic and $I\to B$ is monomorphic, then $A\to I$ is a coimage of $A\to B$ and $I\to B$ is an image of $A\to B$ and for any other such factorization $A\to \overline{I}\to B$ where $A\to\overline{I}$ is epimorphic and $\overline{I}\to B$ monomorphic, there is a unique $I\to\overline{I}$ such that
commutes,
and $I\to\overline{I}$ is necessarily an isomorphism.
But why is $T\to BL$ monic and $TR\to B$ epic?