Find the angles of given triangle ABC

Question

A triangle $ABC$ with angle bisectors $AA_1$ and $BB_1$ is given, such that $\angle AA_1B_1 = 24^\circ$ and $\angle BB_1A_1 = 18^\circ$. Find the angles of the triangle.

I've been stuck on this one for quite a long time. After denoting with $I$ the incenter of ABC and deriving that $\angle C = 96^\circ$ from $\angle AIB = 90^\circ + \frac12\angle C = 138^\circ$, I really don't know how to continue. I tried using Geogebra to see everything clearer or at least guess the answer, and I concluded that $\angle A$ and $\angle B$ should be $12^\circ$ and $72^\circ$ respectively, but I'm not sure how to prove it.

Any help would be appreciated. If I come up with something, I will post it right away. Thanks in advance!

Answer 1

Observe: $2(18°)+24° = \color{red}{60°}$. This hints that maybe producing $18°$ might help. Let $A_1$, $B_1$ respectively denote the point of intersection of angle bisectors from A, B to corresponding sides. Since $\angle ABB_1 = \angle CBB_1$, reflect $∆BA_1B_1$ about side $BB_1$. Let the reflection of $A_1$ on AB be $A'$. Due to the property of reflection, $∆BB_1A_1 ≅ ∆BB_1A'$. Let X denote the point of intersection of $A'A_1$ and $BB_1$. $∆A_1XB ≅ ∆A'XB$, so

$\angle A_1XB = \angle A'XB = \frac{180°}{2} = 90°$.

Therefore, $\angle XA_1A = 90° -(18°+24°) = 48°$

. Observe that $48° = \color{red}{2}×24°$. Since $\angle A_1AB = \angle A_1AC$ reflection $∆A_1AA'$ about line $A_1A$. Let the reflection of $A'$ be $A''$.

$\angle A''A_1A = \angle A'A_1A = 48°$.

Therefore $\angle A''A_1B_1 = 24°$. Let Y denote the point of intersection of $A'B_1$ and $AA_1$. $∆A_1YA' ≅ ∆A_1YA''$. Therefore

$\angle A_1YA'' = \angle A_1YA' = 180°-48°-(90°-18°) = 60°$.

Also $\angle B_1YA = \angle A_1YA' = 60°$. Therefore $\angle B_1YA'' = 180-2×60° = 60°$. Extend $A_1A''$ to a point Z. Observe $B_1$ lies on the angle bisectors of $\angle A''A_1Y$ and $\angle A''YA$. Therefore $A''B_1$ is the angle bisector of $\angle YA''Z$. therefore

$\angle YA''B_1 = 0.5 × (60°+48°) = 54°$.

Therefore

$\angle A_1B_1A'' = 180°-(24°+54°+72°) = 30°$.

$\angle A_1B_1A''$ is exterior angle to $∆A_1B_1A$ therefore $\angle A_1AB_1 = (30°-24°) = 6°$. Therefore $A= 12°$, $B = 72°$, $C=96°$.

Answer 2

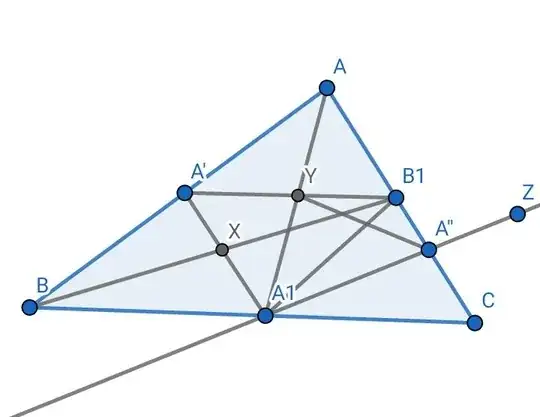
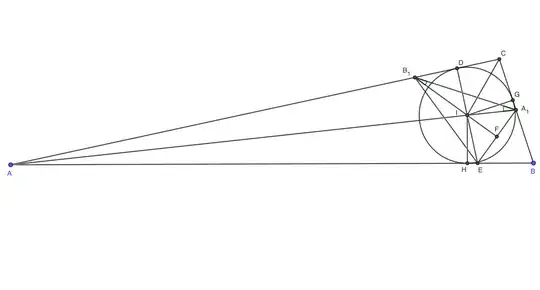
This is not difficult if you use the incenter's property.

Let $\angle CAB=2\alpha$ and $\angle CBA=2\beta$. As we can easily get $\angle C=96^\circ$ we have $\alpha+\beta=42^\circ$.

By the law of sines, we have

$$\frac{IB_1}{IA_1}=\frac{\sin 24^\circ}{\sin 18^\circ}$$

Now we draw perpendicular lines of $IX\perp CA$ and $IY\perp CB$. Since $I$ is incenter, we have $IX=IY$, and thus

$$\frac{\sin 24^\circ}{\sin 18^\circ}=\frac{IB_1}{IA_1}=\frac{IX/\sin(\angle CB_1B)}{IY/\sin(\angle CA_1A)}=\frac{\sin(\angle CA_1A)}{\sin(\angle CB_1B)}=\frac{\sin(2\beta+\alpha)}{\sin(2\alpha+\beta)}$$

Since $\alpha+\beta=42^\circ$, we have $3(\alpha+\beta)=126^\circ$, thus

$$\frac{\sin(2\beta+\alpha)}{\sin(2\alpha+\beta)}=\frac{\sin(126^\circ-(2\alpha+\beta))}{\sin(2\alpha+\beta)}=\sin 126^\circ \cot(2\alpha+\beta)-\cos 126^\circ$$

Notice that $2\alpha+\beta<2(\alpha+\beta)=84^\circ<90^\circ$, we can see $\sin 126^\circ \cot(2\alpha+\beta)-\cos 126^\circ$ as a function of $2\alpha+\beta$ that is monotone in $(0,90^\circ)$. Thus, if we know the function value (which is $\frac{\sin 24^\circ}{\sin 18^\circ}$), there is a unique angle $2\alpha+\beta$. So we can know that there is at most one solution (there is at most one shape). If there is a triangle with ($2\alpha+\beta$) such that

$$\frac{\sin 24^\circ}{\sin 18^\circ}=\frac{\sin(2\beta+\alpha)}{\sin(2\alpha+\beta)}=\frac{\sin(126^\circ-(2\alpha+\beta))}{\sin(2\alpha+\beta)},$$

then that triangle is the desired solution. Now we only need to prove the triangle you proposed satisfies this. That is, if $\angle A=12^\circ$ and $\angle B=72^\circ$ satisfies, this is the only solution.

In this case, $\alpha=6^\circ$, $\beta=36^\circ$. Thus we only need to prove

$$\frac{\sin 24^\circ}{\sin 18^\circ}=\frac{\sin(2\beta+\alpha)}{\sin(2\alpha+\beta)}=\frac{\sin 78^\circ}{\sin 48^\circ}.$$

Or, $$\frac{\sin 24^\circ \sin 48^\circ}{\sin 18^\circ \sin 78^\circ} = 1.$$

This can be proved by following: $$\frac{\sin 24^\circ \sin 48^\circ}{\sin 18^\circ \sin 78^\circ}=\frac{2\sin 12^\circ \cos 12^\circ \sin 48^\circ}{\sin 18^\circ \sin 78^\circ}=\frac{2\sin 12^\circ \sin 48^\circ}{\sin 18^\circ}=\frac{2\sin(30^\circ-18^\circ)\sin(30^\circ+18^\circ)}{\sin 18^\circ}=\frac{2(\sin^2 30^\circ- \sin^2 18^\circ)}{\sin 18^\circ}=\frac{2(\frac{1}{4}- (\frac{\sqrt{5}-1}{4})^2)}{\frac{\sqrt{5}-1}{4}}=\frac{2(\frac{1}{4}- \frac{3-\sqrt{5}}{8})}{\frac{\sqrt{5}-1}{4}}=\frac{\frac{\sqrt{5}-1}{4}}{\frac{\sqrt{5}-1}{4}}=1.$$

Thus, the problem is solved.

---

A friend of mine suggested a geometric method:

Consider the lines

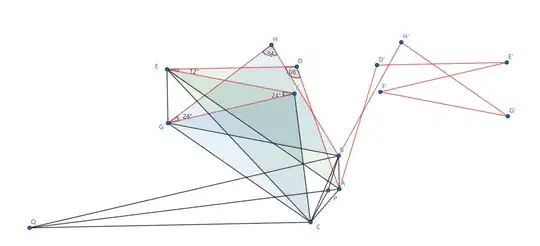
Let a 12-gon $ADEFGHBH'G'F'E'D'A$ (as the figure shows in red lines). twelve liines (in the red) are equal lengths and the angles are: $\angle A=36^\circ$, $\angle D=\angle D'=108^\circ$, $\angle E=\angle E'=12^\circ$, $\angle F=\angle F'=\angle G=\angle G'=24^\circ$, $\angle H=\angle H'=84^\circ$, $\angle B=60^\circ$. One could check, if we go from $A$, and walk through all other vertices along those angles, one will return $A$. This is because (check the angles (don't use the condition $\angle A=36^\circ$, use other angles to derive) and leave as exercise) $\vec{EF}+\vec{G'F'}=0$, $\vec{FG}+\vec{F'E'}=0$, $\vec{DE}+\vec{HB}+\vec{BH'}=0$ (because they are equilateral triangle), and $\vec{AD}+\vec{E'D'}+\vec{D'A}+\vec{H'G'}+\vec{GH}=0$ (because they are regular pentagon.) So this equilateral 12-gon exists and notice that it is symmetry along $AB$, we have $\angle BAD=18^\circ$ and $\angle HBA=150^\circ$.

Then construct $C$ that $GHB$ and $GFC$ are congruent. So we have $\angle EFC=84^\circ$ and thus $\angle EFC=24^\circ+84^\circ=108^\circ=\angle EDA$. So triangle $EDA$ and triangle $EFC$ are congruent. Therefore we have $EA=EC$, $GB=GC$.

We construct $Q$ to be the symmetric point with respect to $EG$. So $EA=EC=EQ$ and $GB=GC=GQ$. So $E$ is the circumcenter of $ACQ$ and $G$ is the circumcenter of $BCQ$. So $$\angle BQC=\angle BGC/2 =\angle HGF/2=12^\circ$$ $$\angle AQC=\angle AEC/2 =\angle FED/2=6^\circ$$ Therefore we have $\angle AQB=6^\circ$ Also we have $\angle FEC=36^\circ$ and $\angle FEG=78^\circ$. Therefore we have $$\angle QAC=\angle QEC/2=\angle GEC=\angle FEG-\angle FEC=42^\circ$$ Also we have $\angle QEC=2\angle GEC=84^\circ$ and $\angle AEC=12^\circ$ $$\angle QAE=90^\circ-(\angle QEA/2)=90^6\circ-(\angle QEC+\angle CEA)/2=90^\circ-(84^\circ+12^\circ)/2=42^\circ$$ So $$\angle BAQ=\angle BAD+\angle DAE+\angle EAQ=18^\circ+36^\circ+42^\circ=96^\circ$$ So $\angle BAC=96^\circ+42^\circ=138^\circ$

Also we have $\angle EGC=\angle EGF+\angle FGC=90^\circ-24^\circ/2+90^\circ-84^\circ/2=126^\circ$, and $\angle GEC=42^\circ$, so $\angle ECG=180^\circ-\angle EGC - \angle GEC=12^\circ$. Since $GB=GC$ and $\angle BGC=24^\circ$, we have $\angle GCB=28^\circ$, so $\angle ECB=66^\circ$. Also, we have $EA=EC$ and $\angle AEC=12^\circ$, we have $\angle ECA=84^\circ$, and thus $\angle BCA=18^\circ$. Therefore we have $\angle ABC=24^\circ$

So we have the configuration: $\angle ABC=24^\circ$, $\angle BCA=18^\circ$, $\angle BAQ=96^\circ$ $\angle QAC=42^\circ$, $\angle BQA=6^\circ$ and $\angle AQC=6^\circ$.

Now we let the circumcircle of $BCQ$ having another intersection of $AQ$, call it $P$. So we have $\angle PBC=\angle PCB=6^\circ$. Thus, we can proof the following lemma:

If the triangle $ABC$ satisfy $\angle B=24^\circ$, $\angle C=18^\circ$, and the interior $P$ such that $\angle PBC=\angle PCB=6^\circ$. We have $\angle PAB=96^\circ$, $\angle PBA=42^\circ$.

This can be proved by the "identity method" and the things above.

Now we turn to the original problem:

Let $P$ be the circumcenter of $B_1CA_1$. Since we have $\angle B_1A_1I=24^\circ$ and $\angle A_1B_1I=18^\circ$, we have $\angle B_1IC_1=138^\circ$, and thus $\angle C=96^\circ$. Therefore, we know that $P$ is the same side with $I$ with respect to $A_1B_1$ and $\angle PA_1B_1=\angle PB_1A_1=6^\circ$. By the lemma above, we have $\angle PIB_1=42^\circ$.

Let $D$ be the intersection of $CI$ and the circumcircle of $CA_1B_1$. We have $\angle PDB_1=\angle B_1DA_1 /2=(180^\circ-\angle C)/2=42^\circ$. Since $\angle PIB_1=42^\circ$, we have $B_1,P,I,D$ four points on a circle. Therefore $\angle PDC=\angle PB_1I=12^\circ$. So we have $\angle CA_1B_1=\angle CDB_1=\angle PDB_1+\angle CDP=54^\circ$. Therefore we know that $\angle CA_1A=24^\circ+54^\circ=78^\circ$ and thus $\angle CAA_1=180^\circ-78^\circ-96^\circ=6^\circ$, so $\angle CAB=12^\circ$, and $\angle ABC=72^\circ$

Answer 3

The following is a kind of reverse approach, beginning with the triangle Euclid uses to construct the regular pentagon. To avoid confusion, and aid comparison, I keep OP's lettering.

Construct triangle $B_1A_1E$ as the $36^o-72^o-72^o$ triangle of Elements IV, 10.

Let $B_1F$ bisect $\angle EB_1A_1$, and make $\angle B_1A_1I=24^o$. Thus $\angle IB_1A_1=\frac{36}{2}=18^o$.

Next make $\angle B_1ID=\angle DIC=42^o$, and make $IC=IB_1$.

Join and extend $CB_1$ to meet $A_1I$ extended at $A$, and join and extend $AE$ and $CA_1$ to meet at $B$.

Since $\angle AIF=138^o$, and if, as OP notes, $\angle ACB=2(138^o-90^o)=96^o$, while $\angle DCI=180^o-(90^o+42^o)=48^o$, therefore also $\angle ICA_1= 48^o$, $CI$ bisects $\angle ACB$, and the incenter of $\triangle ABC$ lies somewhere on $CI$.

Next, dropping perpendiculars $IG$, $IH$, triangles $HIE$ and $GIA_1$ are congruent. For since $\angle DIA=B_1IA+DIB_1=(18+24)+42^o=84^o$, making $\angle AIE=\angle A_1ID=96^o$, while $\angle GID=84^o$, therefore$$\angle A_1IG=96^o-84^o=12^o$$ In like manner$$\angle HIE=\angle AIE-\angle AIH=96^o-84^o=12^o$$

And since by symmetry $IA_1=IE$, then triangles $HIE$ and $GIA_1$ are congruent and$$IH=IG=ID$$

$I$ is thus the incenter of $\triangle ABC$, and $IA$ bisects $\angle CAB$.

And again, since $\angle DIA=84^o$, and $\angle ADI= 90^o$, therefore$$\angle IAD=6^o$$making$$\angle BAC=12^o$$and$$\angle CBA=72^o$$