Sum of uniform random variables, how to systematically convolve distributions

Question

This is a long question/explanation, where I more or less have a method to the madness; however, I've stumbled upon how I perform the calculation and I feel it is quite crude. This question is based off another post about the sum of three variables. Since I'm am unsure of my method, I didn't want to make this an answer there but rather my own question for critiquing. Reproduced here, consider three random variables $X$, $Y$, and $Z$, all drawn from Uniform$(0,1)$. What is the distribution of the sum of the three random variables, $W = X+Y+Z$?

Part 1: Convolution of two variables

First define the random variable of the sum of two variables, $S = X+Y$. We find the pdf of $S$ by convolution of the two distributions

$$\begin{align} f_S(s) &= \int_{-\infty}^\infty\! f_X(s-t) f_Y(t)\ \textrm{d}t,\\ &= \int_0^1\! f_X(s-t)\ \textrm{d}t,\\ &= \int_{s-1}^s f_X(u)\ \textrm{d}u. \end{align}$$

Here I used the fact that $f_Y(t) = 1$ when $0 \leq t \leq 1$, and is otherwise $0$. Likewise, we know that $f_X(s-t)$ has the same properties, such that another bound is $0 \leq s-t \leq 1$. This may be transform into $s-1 \leq t \leq s$, which is "coincidently" the bounds over the variable $u$ (perhaps this "coincident" is where my enlightenment awaits).

$\textbf{Here}$ is where I make a leap of faith of sorts. We now have two bounds for for our integral over $t$

1. $0 \leq t \leq 1$ from the pdf of $Y$, and
2. $s-1 \leq t \leq s$ from the shifted pdf of $X$.

I therefore, "mix-and-match" my bounds to arrive at

$$\begin{align} f_S(s) = \cases{ \displaystyle\int_0^s \mathrm{d}t = s, & $0 \leq s < 1$\\ \displaystyle\int_{s-1}^1 \mathrm{d}t = 2-s, & $1 \leq s \leq 2$ }. \end{align}$$

I can see the mixing of bounds either from naively swapping them (say the upper bounds). I can also appreciate from visualizing the convolution that there are two "behaviors" and therefore a piecewise function is appropriate. However, this feeling is not systematized and is just an intuition at best. I've seen these bounds explained via proof by "what else could it be", i.e., what makes sense to keep the integral within the domain $[0,1]$, where we take that $s \in [0,2]$ since $S = X+Y$... After arriving at the answer that seems fine, but not very satisfactory.

Aside about how I visualize the convolution

Imagining the convolution of the two unit boxes, fixing one distribution and sliding the other, there are three "moments"/instances of interest

1. When the distributions begin to overlap, the leading edge of the sliding distribution is at $s=0$.
2. When the distributions completely overlap, $s=1$. This moment also coincides with when the distributions begin to diverge.
3. When the distributions last touch $s=2$.

Since "moment" two is instantaneous there are really only two "event," when the distributions are increasing their overlapping region and when the are decreasing it. From this, I argue there are two cases: $0 \leq s < 1$ and $1 \leq s \leq 2$.

Part 2: Convolution of three variables

We now want $W = X+Y+Z = S+Z$, meaning we will use our results from the convolution of two variables to do another convolution. Similar to before

$$\begin{align} f_W(w) &= \int_{-\infty}^\infty\! f_S(w-t) f_Z(t)\ \textrm{d}t,\\ &= \int_0^1\! f_S(w-t)\ \textrm{d}t,\\ &= \int_{w-1}^w f_S(u)\ \textrm{d}u. \end{align}$$

Here again I have restricted $0 \leq t \leq 1$ from the distribution of $Z$. Now this time $f_S(w-t)$ is a little more complicated since it is not a uniform distribution

$$\begin{align} f_S(w-t) = \cases{ w-t, & $0 \leq w-t < 1\ \longrightarrow\ w-1 \leq t \leq w$\\ 2-w+t, & $1 \leq w-t \leq 2\ \longrightarrow\ w-2 \leq t \leq w-1$ }. \end{align}$$

Now I can repeat the "mixing-and-matching" of $0 \leq t \leq 1$ with the bounds of $f_S$ to arrive at a list of

1. $0 \leq t \leq w$
2. $w-1 \leq t \leq 1$
3. $0 \leq t \leq w-1$
4. $w-2 \leq t \leq 1$.

Now I have to lean on my visualization of the convolution to say there are three cases of interest. These are, with what bounds I associated with them, when the distribution begin to overlap (1), while the overlap (2 and 3), and when the begin to stop overlapping (4). Thus, the first half of $f_S$ shows up by itself while they begin to overlap, both part of $f_S$ contribute while the distributions are completely overlapping, and only the later part of $f_S$ contributes when they begin to diverge. This leads me to the result that

$$\begin{align} f_W(w) = \cases{ \displaystyle\int_0^w (w-t)\ \mathrm{d}t = \frac{w^2}{2}, & $0 \leq w < 1$\\ \displaystyle\int_{w-1}^1 (w-t)\ \mathrm{d}t + \int_0^{w-1} (2-w+t)\ \mathrm{d}t= -w^2 + 3w - \frac{3}{2}, & $1 \leq w \leq 2$\\ \displaystyle\int_{w-2}^1 (2-w+t)\ \mathrm{d}t= \frac{(w-3)^2}{2}, & $2 \leq w \leq 3$ }. \end{align}$$

This is the correct answer from the original post. My intuition hasn't gotten me the wrong answer at the very least.

Part 3: Convolution of four variables

I'll skip the majority of the explanation, and summarize we now want $K = X+Y+Z+J$, where $J$ is another random variable drawn from Uniform$(0,1)$.

$$\begin{align} f_K(k) &= \int_{-\infty}^\infty\! f_W(k-t) f_J(t)\ \textrm{d}t,\\ &= \int_0^1\! f_W(k-t)\ \textrm{d}t,\\ &= \int_{k-1}^k f_W(u)\ \textrm{d}u. \end{align}$$

Writing the shifted convolved three variable distribution and solving for its bounds

$$\begin{align} f_W(k-t) = \cases{ \frac{(k-t)^2}{2}, & $0 \leq k-t < 1\ \longrightarrow k-1 \leq t < k$\\ -(k-t)^2 + 3(k-t) - \frac{3}{2}, & $1 \leq k-t \leq 2\ \longrightarrow k-2 \leq t < k-1$\\ \frac{(k-t-3)^2}{2}, & $2 \leq k-t \leq 3\ \longrightarrow k-3 \leq t < k-2$ }. \end{align}$$

Then setting up the integrals and solving I arrive at

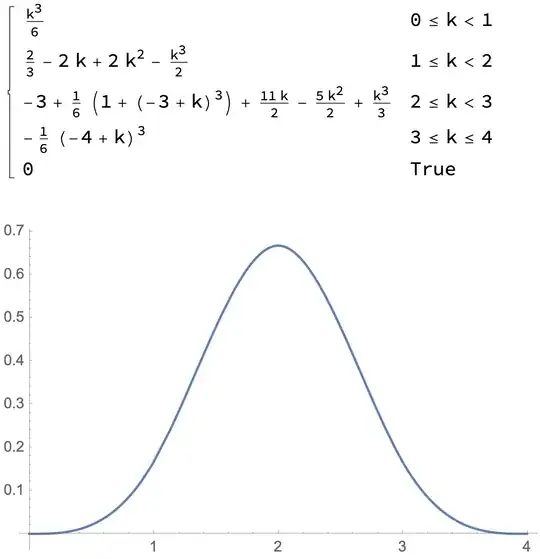
$$\begin{align} f_K(k) = \cases{ \displaystyle\int_0^k \frac{(k-t)^2}{2}\ \mathrm{d}t = \frac{k^3}{6}, & $0 \leq k < 1$\\ \displaystyle\int_{k-1}^1 \frac{(k-t)^2}{2}\ \mathrm{d}t + \int_0^{k-1} \left(-(k-t)^2+3(k-t)-\frac{3}{2}\right)\ \mathrm{d}t= -\frac{k^3}{3} + 2 k^2 - 2k + \frac{2}{3}, & $1 \leq k < 2$\\ \displaystyle\int_{k-2}^1 \left(-(k-t)^2+3(k-t)-\frac{3}{2}\right)\ \mathrm{d}t + \int_0^{k-2} \frac{(k-t-3)^2}{2}\ \mathrm{d}t = \frac{k^3}{2} -4k^2 +10k - \frac{22}{3}, & $2 \leq k < 3$\\ \displaystyle\int_{k-3}^1 \frac{(k-t-3)^2}{2}\ \mathrm{d}t = -\frac{(k-4)^3}{6}, & $3 \leq k \leq 4$\\ }. \end{align}$$

Now this is where my earlier visualization intuition failed me, or at least evidently needed to be tweaked. Rather than the events: beginning to overlap, overlapping, and beginning to diverge; the real importance is the coupling of different regions. Meaning, the first piecewise in the 2 variable sum came from coupling the void (0) with the first half of the uniform distribution, and the void with the second half—this seems to be the biggest subtly in my altered thinking. However, it is then straightforward to see why we have 3 pieces for the 3 sum, and 4 for the 4 sum, and why each middle section is the sum of two integrals as we are coupling adjacent regions. In fact all pieces are the sum of two integrals, it is just that the first and last section are integrals over 0!

Now I have no reference for if these are correct, but it is what I get from following my method. Moreover, when I plot it in Mathematica, I got a reasonable looking distribution. By chance if this process is taken to infinitum, does this converge to a scaled Normal distribution (perhaps rather the of convolving the Uniform$(-1,1)$)? I'd suppose not exactly, as the convolution of the normal with a uniform is not strictly the normal distribution from what I've seen.

Question/Challenge

With my thinking made clear, I am having difficulty convolving the triangle distribution with itself, i.e., it should be our 4 uniform variable sum. Now I want to see that $K = S+S$ such that

$$\begin{align} f_K(k) &= \int_{-\infty}^\infty\! f_S(k-t) f_S(t)\ \textrm{d}t,\\ &= \int_0^1\! t f_S(s-t)\ \textrm{d}t + \int_1^2 (2-t) f_S(s-t)\ \textrm{d}t. \end{align}$$

How are the bound picked, and how do I systematically know which integrals combine with one another? I can get the limits $0 \leq t \leq 2$, $z-1 \leq t \leq z$ and $z-2 \leq t \leq z-1$. Naively, I can end up with 8 integrals, four for each term in $f_K(k)$ where I get four from mixing and matching bounds of the shifted triangle distribution. If there are really 8 integrals, which ones belong to which section of the piecewise function?

Answer 1

The core of this problem is how to systematically convolve 2 piecewise functions, which doesn't necessarily involve probability distributions per se.

This manuscript, which is also motivated by summing uniform random variables, provides such a method: http://www.mare.ee/indrek/misc/convolution.pdf

The essential ideas are copied below:

Part 1: Each function is only defined on 1 interval

Given 2 functions $F(x)$ and $G(x)$ such that $$ F(x)=\begin{cases} f(x), & a_f < x < b_f\\ 0, & \text{otherwise} \end{cases} $$ $$ G(x)=\begin{cases} g(x), & a_g < x < b_g\\ 0, & \text{otherwise} \end{cases} $$ We can assume without the loss of generality that $b_f - a_f < b_g - a_g$, because convolution is commutative and we can convert $F * G$ to $G * F$ when necessary.

$$ \begin{align*} (F*G)(t) &= \int_{-\infty}^\infty F(x)G(t-x)\ dx\\ &= \int_{-\infty}^\infty F(x)G(t-x)\ dx\\ &= \begin{cases} \int_{a_f}^{t - a_g} f(x)g(t-x)\ dx, & a_f + a_g < t < b_f + a_g\\ \int_{a_f}^{b_f} f(x)g(t-x)\ dx, & b_f + a_g < t < a_f + b_g\\ \int_{t-b_g}^{b_f} f(x)g(t-x)\ dx, & a_f + b_g < t < b_f + b_g\\ 0, & \text{otherwise} \end{cases} \end{align*} $$

Part 2: Multiple Intervals

Given piecewise functions with non-overlapping intervals: $$ F(x) = \begin{cases} f_1(x), & a_f^1 < x < b_f^1\\ ...\\ f_N(x), & a_f^N < x < b_f^N\\ 0, &\text{otherwise} \end{cases}\\ G(x) = \begin{cases} g_1(x), & a_g^1 < x < b_g^1\\ ...\\ g_N(x), & a_g^M < x < b_g^M\\ 0, &\text{otherwise} \end{cases} $$

We can rewrite $F(x) = \sum_{i=1}^N F_i(x)$ where $$F_i(x) = \begin{cases} f_i(x), & a_f^i < x < b_f^i\\ 0, & \text{otherwise} \end{cases} $$

Because convolution is distributive with respect to addition $f * (g + h) = f*g + f*h$, we can calculate $F*G$ as follows $$ F*G = \sum_{i=1}^N \sum_{j=1}^M F_i * G_j $$

Going back to your original question. We can find the intervals for $t$ based on the intervals $(a_f, b_f)$ and $(a_g, b_g)$. When there are multiple intervals, the problem reduces to the sum of piecewise functions, which is just finding overlaps of intervals.

Answer 2

Since this was an ill posed question, and I tried to throw in a concrete question at the end, I've answered it myself (as to not waste anyone's time further). The 8 integrals I got are:

$$\begin{align} 1.& \int_0^z t(z-t)\ \textrm{d}t, &0 \leq z < 1,\\ 2.& \int_{z-1}^1 t(z-t)\ \textrm{d}t, &1 \leq z < 2,\\ 3.& \int_0^{z-1} t(2-z+t)\ \textrm{d}t, &1 \leq z < 2,\\ 4.& \int_{z-2}^1 t(2-z+t)\ \textrm{d}t, &2 \leq z < 3,\\ 5.& \int_1^z (2-t)(z-t)\ \textrm{d}t, &1 \leq z < 2,\\ 6.& \int_{z-1}^2 (2-t)(z-t)\ \textrm{d}t, &2 \leq z < 3,\\ 7.& \int_1^{z-1} (2-t)(2-z+t)\ \textrm{d}t, &2 \leq z < 3,\\ 8.& \int_{z-2}^2 (2-t)(2-z+t)\ \textrm{d}t, &3 \leq z \leq 4. \end{align}$$

The first four come from the first term, while the last four come from the second term of the convolution. These integrals were got from mixing and matching, and which part of the piecewise function they belonged to were argued from what else could they be, i.e., the only values that are valid. This indeed reduces to the sum of 4 uniform random variables. Hopefully, the pattern is evident to anyone who stumbles across this post hoping to understand convolution.

I suppose I am satisfied that I can do convolutions; however, I more than happily will accept an answer that gives better insight other than "what else could they be."