It is a known fact that floating point precision errors are bound to happen when one forces a computer to deal with very large or very small numbers, especially when both things are done at the same time. I was playing around with similar functions as the one described in this question, that is functions of the type: $$ g(f(x))=\left(1+\frac{1}{f(x)}\right)^{f(x)} \\ $$ With $\lim_{x\to +\infty}{f(x)}=+\infty$ and $f(x)$ a "rapidly" growing function of $x$, such as $e^{x}$, $\Gamma(x+1),x^{9}$ and so on. For each and everyone of these functions the plot I have behave similarly, as shows the first figure. I don't understand the zig-zag behavior very well, but the jump to 1 is easy to understand: $\frac{1}{f(x)}$ becomes so small that the computer treats it as $0$.
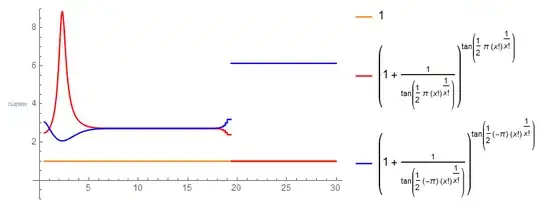
That all said, here comes the surprising stuff. It is known that $\lim_{x\to\infty}x^{1/x}=1$, and so $\lim_{x\to\infty}{\Gamma(x+1)^{\frac{1}{\Gamma(x+1)}}}=1$. Hence $tan\left(\pm\frac{\pi}{2}\Gamma(x+1)^{\frac{1}{\Gamma(x+1)}}\right)$ should also go to infinity (in modulus, at least) with $x$. When I plot $g(f(x))$ with this tangent thing as $f$, numeric precision problems also disrupt the function, but they do so in a pretty strange way, as shows the second figure (I added a line for $1$ for comparison). There's no zig-zag (which doesn't trouble me that much actually), but only the function with a positive sign collapses into $1$, the negative collapses into $\approx 6.12961$.
Does anyone know why this particular function has such a strange behavior? Or at least what kind of material should I read to in order to discover the answer?
Is it possible to work out why it collapses into this particular number? Can we find other similar examples? Thank you!