Can we count or even recursively construct all ways to tile or partition a rectangle with rectangles? Many other questions ask either of two things none of which I am after:
- Partitioning a rectangle by vertical or horizontal lines, like in Number of ways to partition a rectangle into n sub-rectangles.
- Tiling a rectangle with some prescribed tiles.
My question pertains to all the ways to partition a rectangle such that all partitions are rectangles in itself. I think (1) above does not cover this because of
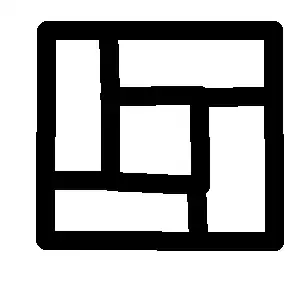for which I think there is no way to create it incrementally by adding straight lines that partition the original or a sub-rectangle.
So let me try to describe which partitions I would like to count and ideally construct:
- An outer rectangle shall be partitioned into rectangles.
- The size of the outer or the inner rectangles is not important, so shifting a common side of inner rectangles does not create a new configuration as long as the size is not zero. (I might be missing corner cases here.)
- Whether mirroring (flipping) or rotational symmetries shall count separately, I don't mind. Whatever is easier to describe.
I suspect that up until 4 inner rectangles, the result is the same as described in the question cited above, but my drawing shows that latest from 5 inner rectangles, the solutions are no longer the same.
