Alternate non-sum form or integral representation of $\sum_{x\in \Bbb Z} (-1)^x \left(x^\frac1x -1\right)$.

Question

I was inspired from this problem with an integral of an infinite tetration. I saw that you can do this series for the infinite tetration with an analytic continuation. However, the

Here is the sum with some terminology:

$$\mathrm{R=\sum_{x\in \Bbb Z} (-1)^x \left(x^\frac1x -1\right)= \sum_{0\ne x\in \Bbb Z} (-1)^x \left(x^\frac1x -1\right) +\lim_{x\to 0^+} (-1)^x \left(x^\frac1x -1\right)=-1+\sum_{0\ne x\in \Bbb Z} (-1)^xx^\frac1x -\sum_{0\ne x\in \Bbb Z} (-1)^x=.5645…-.3787…i }$$

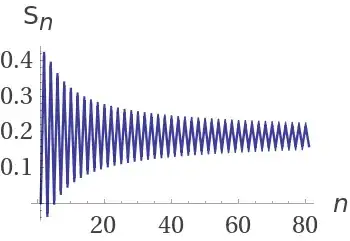
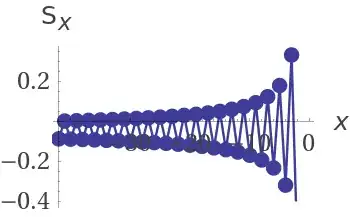
This converges using the alternating series test from this graph or simply do interval testing to find an increasing function on [0,e] and decreasing on [e,$\infty$]. For the negative branch, the function decreases to zero for the real and imaginary parts as seen here. As said before, the function approaches zero from both sides and therefore, R exists by the alternating series test. Here are some partial sum graphs excluding x$\to$ 0=-1. The negative sum converges as seen here:

If we could evaluate the sum, then we could get a solution. This seems unlikely to get a closed solution without a sum, therefore, this will be an answer to some integral. This looks like it could be a sophomore dream like problem.

Of course we can easily do $$\mathrm{R=\int_0^R dx=\int \sum_{x\in \Bbb Z} \frac d{dx}(-1)^x \left(x^\frac1x -1\right)dx}$$ but it was hoped to find a definite integral which is not obvious like the one from 0 to R of y=1.

If the sum was taken over positive x, for x>2 as the summand value for x=1 is 0, then $$\mathrm{R_+= \sum_{x=2}^\infty (-1)^x \left(x^\frac1x -1\right)=-.187… }$$

I could also try to find a representation term by term, but that would be tedious. What is an integral representation or alternate non-sum representation of R or $\mathrm R_+$? Please give me feedback and correct me!

I did find this using the derivative like Feynman Integration:

$$\mathrm{R_+=\sum_{a=2}^\infty \int_0^a\frac{cos(\pi x)x^{\frac1a-1}}{a}+i\pi cos(\pi x)\left(x^\frac1a-1\right)dx}$$

Answer 1

After @GottfreidHelms posted the correct decimal approximation, I put this into a closed form searcher and saw immediately this was the MRB Constant. Let this constant be denoted as r=$R_+$ for its original name of “root constant”. Then, the sum of R can be found to be the following after some tinkering. The summation converges slowly because of oscillation. Here is a computation with work and conjectured results. Note the “$1+ 2r$” is related to OEIS A173273:

$$\mathrm {Re(R_-)=Re\sum_{n=-\infty}^{-1}(-1)^x\left(x^\frac1x-1\right)=1+2r,Im(R_-)=-2r\implies R=-1+1+2r-2r\mathit i=3r-2r\mathit i=r(3-2\mathit i)= 0.56357892738620136074555380216281969016770928470041635851601405226843169469... - 0.37571928492413424049703586810854646011180618980027757234400936817895446312... i=(2+3\mathit i)\int_{-\mathit i\infty}^\mathit i csc(\pi x)Im\left(\sqrt[x]x\right)dx=(3-2\mathit i)\int_{\Bbb R^+}csch(\pi x)Im\left((1+\mathit ix)^{\frac1{1+\mathit ix}}\right)dx}$$

The integral representation comes from the alternating version of the Abel Plana formula? I am not sure how to evaluate this nor the one posted in Wolfram Mathworld with real integration bounds. The imaginary part complicates matters too. However, please correct me and give me feedback!