Difficulty in understanding the proof of Petersen Graph is non hamiltonian as given in graph theory text by Chartrand and Zhang

Question

I was going through the text : A First Course in Graph Theory by Chartrand and Zhang where I could not understand a few statements in the proof. Below is the excerpt:

Theorem 6.4 : Petersen graph is non-Hamiltonian

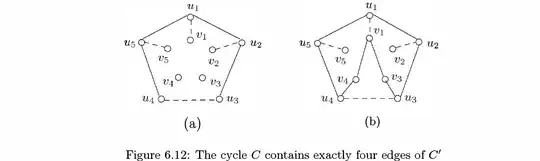
Proof : Suppose that the Petersen graph, which we will denote by PG, is Hamiltonian. Then PG contains a Hamiltonian cycle $C$. This cycle contains ten edges. Two of the three edges incident with each vertex of PG necessarily belong to $C$. Certainly, $C$ contains all, some or none of the five edges $u_iv_i (1\leq i\leq 5)$; so at least five edges of $C$ belong to either $C'$ or to $C''$/ Therefore, either $C'$ contains at least three edges of $C$ or $C''$ contains at least three edges of $C$. First, observe that all five edges of $C'$ cannot belong to $C$ since no cycle contains a smaller cycle as a subgraph. Suppose that $C$ contains exactly four edges of $C'$, say the edges $u_4u_5, u_5u_1, u_1u_2, u_2u_3$ (see figure- 6.12(a), where the dashed edges of PG cannot belong to $C$). However the cycle $C$ must then contain the edges $u_4v_4, u_3v_3$ as well as $v_1v_3, v_1v_4$ (see figure 6.12 (b)). But this implies that C contains an $8$ cycle which is impossible.

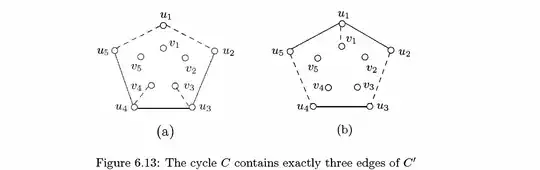
One case remains then, namely that $C$ contains exactly three edges of $C′$. There are two possibilities: $(1)$ the three edges of $C′$ on $C$ are consecutive on $C′$ or $(2)$ these three edges are not consecutive on $C′$. These possibilities are shown in Figures 6.13(a) and 6.13(b), respectively. The situation in Figure 6.13(a) is impossible as $u_1v_1$ is the only edge incident with $u_1$ that could lie on $C$.Likewise, the situation in Figure 6.13(b) is impossible since $C$ would have to contain the smaller cycle $(u_4, v_4, v_1, v_3, u_3, u_4)$. Therefore, as claimed, the Petersen graph is not Hamiltonian. $\square$

The text assumes $C': u_1,u_2, u_3,u_4,u_5$, $C'': v_1,v_2, v_3,v_4,v_5$

Can anyone explain to me the lines of the proof given in bold?

Answer 1

The Petersen graph has three sorts of edges in the usual picture: Those in $C'$ (the outer pentagon), those in $C''$ (the inner pentagram), and those of the form $u_iv_i$ joining the inner to the outer part. If $C$ were a Hamiltonian cycle, it would contain 10 edges (because PG has 10 vertices). At most 5 of those edges in $C$ could be of the $u_iv_i$ sort (as there are only 5 such edges altogether), so that leaves at least 5 other edges in $C$ that are in $C'\cup C''$. One of $C'$ and $C''$ must contain at least 3 of these edges from $C$ because, if they each contained only 2 or fewer, that would be only 4 or fewer edges, not the required "at least 5". That's what the bold part says.

Answer 2

If you prefer, here is an alternate proof that may be easier to understand than Chartrand and Zhang's. (That's a matter of taste, but at least it's shorter.)

---

If we color the edges of the Hamiltonian cycle by alternating blue and orange, and color the five leftover edges purple, we'll get a proper $3$-edge-coloring of the Petersen graph: each vertex will be incident on a blue, orange, and purple edge. (There are five edges of each color.) We can show that such a thing cannot exist.

The outer cycle has $5$ edges, and each color can appear on at most $2$ of them, so its colors must be split $2$-$2$-$1$. Since there is symmetry between the colors, let's say there's two blue edges, two orange edges, and one purple edge. Since there is symmetry between the edges of the cycle, let's say $u_1 u_2$ is the purple edge, in Chartrand and Zhang's notation.

Then $u_3, u_4, u_5$ need their own purple edges. To make this happen, $u_3 v_3$, $u_4 v_4$, and $u_5 v_5$ must be purple.

We've found four out of five purple edges, and vertices $u_1, u_2, u_3, u_4, u_5, v_3, v_4, v_5$ are already incident on a purple edge. The remaining purple edge must cover vertices $v_1$ and $v_2$, but this is impossible, since $v_1$ and $v_2$ are not adjacent.

---

Here is an alternate alternate proof inspired by bof's solution. It's now redundant, given that bof's answer has been rewritten to do the same thing more generally, but I'll leave this up on the theory that two explanations are better than one.

Suppose we have a $10$-vertex cubic graph that consists of a Hamiltonian cycle $v_1 v_2 \dots v_{10} v_1$ and a matching. Then we'll show that it must contain a $3$-cycle or a $4$-cycle, which the Petersen graph does not. (Conversely, the Petersen graph cannot have a Hamiltonian cycle.) There are three cases for the matching we add:

• If a vertex is matched to another vertex $2$ or $3$ steps around the cycle (such as $v_1$ to $v_3$, $v_4$, $v_8$, or $v_9$) that automatically creates a $3$-cycle or $4$-cycle.
• Otherwise, if a pair of opposite vertices such as $v_1$ and $v_6$ are not matched together, then $v_1$ is matched to $x \in \{v_5, v_7\}$ and $v_{6}$ is matched to $y \in \{v_2, v_{10}\}$, and no matter which choice for $x,y$ is picked, $v_1 x v_6 y v_1$ is a $4$-cycle.
• Otherwise, if all opposite vertices are matched together, then $v_1 v_6 v_7 v_2 v_1$ is a $4$-cycle.

Answer 3

(This is a simplified and generalized version, based on a comment by Misha Lavrov, of the answer originally posted in this space.)

If you just need a proof of the fact that the Petersen graph is not Hamiltonian, here is a simple proof of a somewhat more general proposition. Recall that the Petersen graph is a cubic graph of order $10$ and girth $5$.

Proposition. For $n\ge2$ a cubic graph of order $4n+2$, girth $g\gt2n$, and chromatic number $\chi\gt2$ is not Hamiltonian.

Proof. Suppose $G$ is a Hamiltonian cubic graph of order $4n+2$ and girth $g\gt2n\ge4$; I will show that $G$ is bipartite.

The graph $G$ may be constructed by adding a matching to the cycle graph $C_{4n+2}$. Label the vertices $v_0,v_1,\dots,v_{4n+1}$ in their order along the cycle.

Since $g\gt2n$, the vertex $v_0$ must be matched with $v_{2n}$ or $v_{2n+1}$ or $v_{2n+2}$. However, if $v_0$ is matched with $v_{2n+2}$, then $v+1$ can't be matched at all without creating a cycle of length less than $g$, since $g\ge4$. Therefore $v_0$ can't be matched with $v_{2n+2}$, and by the same token it can't be matched with $v_{2n}$, it can only be matched with the diametrically opposite vertex $v_{2n+1}$. Likewise, every vertex $v_i$ must be matched with the diametrically opposite vertex. It follows that $G$ is a bipartite graph; every edge joins a vertex with even index to a vertex with odd index.