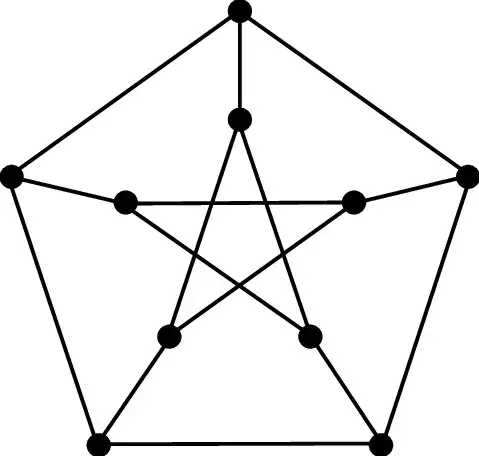
Petersen's Graph
Is there a path of length $10$ in the Petersen's graph? If so, is it true that Petersen's graph would be Hamiltonian? Is the fact that each vertex has degree $3$ fundamental to disprove the previous statement; because if I start at a vertex $v_0$, then I should come back to it by the end of my path, but this would imply that we didn't pass by one edge that is one of three incident edges to the vertex $v_0$. Any suggestions?