Does a non-trivial solution exist for $f'(x)=f(f(x))$?

Question

Does $f'(x)=f(f(x))$ have any solutions other than $f(x)=0$?

I have become convinced that it does (see below), but I don't know of any way to prove this.

Is there a nice method for solving this kind of equation? If this equation doesn't have any non-trivial solutions, do you know of any similar equations (i.e. involving both nested functions and derivatives) that do have interesting solutions?

---

If we assume $f$ is analytic (which I will be doing from this point onward), then it must also be injective (see alex.jordan's attempted proof), and therefore has at most one root (call it $x_0$.)

We know $f'(x_0)=f(f(x_0))=f(0)$.

---

Claim: $f$ cannot have a positive root.

Suppose $x_0$ is positive. If $f(0)$ is negative, then for some sufficiently small $\delta>0$, $f(x_0-\delta)>0$. This implies there must be another root between $x_0$ and $0$, but $f$ has at most one root.

The same reasoning applies if $f(0)$ is positive.

If $f(0)=0$, then both $x_0$ and $0$ are roots. Thus, we conclude that $x_0$ cannot be positive.

---

Claim: $f$ cannot have zero as a root.

Suppose $x_0=0$. Since $f$ has at most one root, we know $f$ will be of constant sign on each of the positive and negative halves of the $x$ axis.

Let $a<0$. If $f(a)<0$, this implies $f'(a)=f(f(a))<0$, so on the negative half of the real line, $f$ is negative and strictly decreasing. This contradicts the assumption that $f(0)=0$. Therefore, $a<0\implies f(a)>0$, which then implies $f'(a)<0$.

But since $f'(a)=f(f(a))$, and $f(a)>0$, this implies $f(b)<0$ when $b>0$. Moreover, we know $f'(b)=f(f(b))$, and $f(b)<0 \implies f(f(b))>0$, so we know $f$ is negative and strictly increasing on the positive half of the real line. This contradicts the assumption that $f(0)=0$.

---

Claim: $f$ is bounded below by $x_0$ (which we've proved must be negative if it exists)

We know $f(x_0)=0$ is the only root, so $f'(x)=0$ iff $f(x)=x_0$. And since $f$ is injective, it follows that $f$ is either bounded above or bounded below by $x_0$ (if $f$ crossed $y=x_0$, that would correspond to a local minimum or maximum.) Since $f(x_0)=0$ and $x_0<0$, we know $x_0$ must be a lower bound.

---

Claim: $f$ is strictly decreasing.

Question B5 from the 2010 Putnam math competition rules out strictly increasing functions, so we know $f$ must be strictly decreasing.

---

Claim: $f$ has linear asymptotes at $\pm \infty$

Since $f$ is strictly decreasing and bounded below by $x_0$, we know $\lim_{x\rightarrow\infty}f(x)$ is well defined, and $\lim_{x\rightarrow\infty}f'(x)=0$. Since $f'(x)=0$ iff $f(x)=x_0$, it follows that $\lim_{x\rightarrow\infty}f(x)=x_0$.

$f''(x)=\frac{d}{dx}f'(x)=\frac{d}{dx}f(f(x))=f'(f(x))f'(x)$. Since $f'(x)<0$, we know $f$ is concave up. Thus, $\lim_{x\rightarrow -\infty}f(x)\rightarrow\infty$. This in turn implies $\lim_{x\rightarrow -\infty}f'(x)=\lim_{x\rightarrow -\infty}f(f(x))=\lim_{x\rightarrow \infty}f(x)=x_0$.

So $f$ goes to $x_0$ when $x\rightarrow\infty$, and approaches the asymptote $y=x_0\cdot x$ when $x\rightarrow-\infty$.

---

Claim: $x_0<1$

Consider the tangent line at $f(x_0)$. We know $f'(x_0)=f(0)$, so this line is given by $y=f(0)x-f(0)x_0$. Since $f$ is concave up, we know $f(x) > f(0)x-f(0)x_0$ for $x\neq x_0$, so $f(0) > -f(0)x_0$. And we can conclude $x_0<-1$.

---

Claim: $f$ must have a fixed point, $x_p$ (i.e. $f(x_p)=x_p$)

We know $f(x_0)=0$, $x_0<0$, and $f(0)<0$. Therefore, $f(x)-x$ has a root in the interval $(x_0,0)$.

---

This is all I have been able to prove. However, the existence of a fixed point turns out to be very useful in constructing approximate solutions.

Consider the following:

$$f(x_p)=x_p$$ $$f'(x_p)=f(f(x_p))=x_p$$ $$f''(x_p)=f'(f(x_p))f'(x_p)=f(f(f(x_p)))f(f(x_p))=x_p^2$$ $$f'''(x_p)=\cdots=x_p^4+x_p^3$$

If we are willing to put in the work, we can evaluate any derivative at the fixed point. I wrote a python program that computes these terms (unfortunately it runs in exponential time, but it's still fast enough to compute the first 20 or so terms in a reasonable amount of time). It leverages the following bit of information.

Suppose $f^{[n]}$ represents the nth iterate of $f$. e.g. $f^{[3]}=f(f(f(x)))$. Then we can derive the following recursive formula.

$$\frac{d}{dx}f^{[n]}=f'(f^{[n-1]})\frac{d}{dx}f^{[n-1]}=f^{[n+1]}\frac{d}{dx}f^{[n-1]}$$

And since we know the base case $\frac{d}{dx}f^{[1]}=f^{[2]}$, this lets us determine $(f^{[n]})'=f^{[n+1]}f^{[n]}\cdots f^{[3]}f^{[2]}$.

So, if we choose a fixed point, we can calculate the expected Taylor series around that point.

Here's the graph for the Taylor series with 14 terms, calculated with fixed point $-0.6$

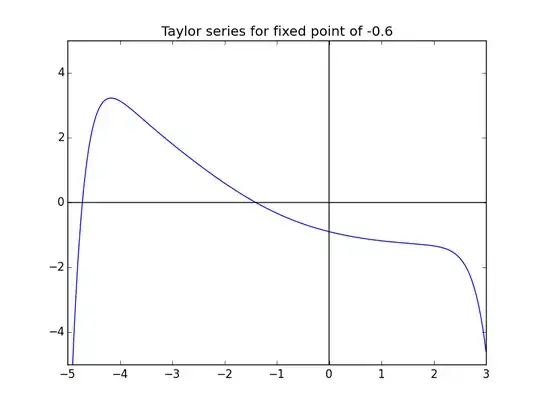
You can clearly see the points where the series starts to fail (the radius of convergence doesn't seem to be infinite), but elsewhere the approximation behaves just as we would expect.

I computed $(P'(x)-P(P(x)))^2$, where $P$ is the Taylor polynomial, over the range where the series seems to converge, and the total error is on the order of $10^{-10}$. Moreover, this error seems to get smaller the more accurately you compute the derivative (I used $P'(x)\approx\frac{P(x+0.001)-P(x-0.001)}{0.002}$).

Answer 1

Given any $a > 0$, there is a unique function $f\colon\mathbb{R}\to\mathbb{R}$ satisfying $f^\prime(x)=f(f(x))$ and $f(-a)=-a$.

[Note: Separately, it can be shown that the only solution with $f(0)=0$ is the trivial one, and all solutions are decreasing, so this lists all possible solutions of $f^\prime(x)=f(f(x))$ on $\mathbb{R}$.]

The idea is that we can view $f^\prime(x)=f(f(x))$ as a differential equation starting at $x=-a$ and solving this to extend $f$ to the left (and right) of the fixed point. However, if $f$ is decreasing, then it maps points on the left of $-a$ to the right and vice-versa. So, we have to extend simultaneously to the left and the right of $-a$ giving a coupled pair of differential equations. If we set $g(x)=f(f(x))$ then we have $g^\prime(x)=f(f(f(x)))f(f(x))$, giving the coupled equations, \begin{align} &f^\prime(x)=g(x),\\ &g^\prime(x)=f(g(x))g(x). \end{align} We can then solve this ordinary differential equation with starting point $x=-a$ and extend to all $x \le -a$. I will change variables in order to convert this to an ODE starting at $x=0$ by setting $u(x)=f(-x-a)+a$ and $v(x)=-a-g(-a-x)$, then these must satisfy $$ \begin{align} &u^\prime(x)=a+v(x)\\ &v^\prime(x)=(a+v(x))(a-u(v(x))). \end{align}{\ \ \ \rm(1)} $$ The idea of the proof will be to show that (1) has a unique solution over $x\in[0,\infty)$ such that $u(0)=v(0)=0$ and, furthermore, that $u,v$ are then strictly increasing with $u(x)\to\infty$ as $x\to\infty$.

As we have noted, if $f'(x)=f(f(x))$ and $f(-a)=-a$ then $u(x)=f(-a-x)+a$ and $v(x)=-a-f(-a+u(x))$ satisfy (1). So, uniqueness of (1) together with the fact that $u(x)\to\infty$ as $x\to\infty$ implies that $f$ is uniquely defined on $\mathbb{R}$ by $$ \begin{align} &f(-a-x)=-a+u(x),\\ &f(-a+u(x))=-a-v(x) \end{align}\ \ {\rm(2)} $$ for $x\ge0$.

Conversely, suppose we have solutions to (1). Defining $f$ on $\mathbb{R}$ by (2) (over $x\ge0$), then it is straightforward to differentiate these and verify that $f^\prime(x)=f(f(x))$.

---

Let us now prove existence and uniqueness for (1). First, suppose that $u,v$ is a solution to (1). Then, considering the ODE for $v$ by itself, we have $v^\prime=F(v)$ where $F(v)=(a+v)(a-u(v))$ is a differentiable (hence, locally Lipschitz) function. We cannot have $F(v(x_0))=0$ for any $x_0>0$ otherwise, by the Picard–Lindelöf theorem for uniqueness of solutions to ODEs, $v$ would have to be constant, giving the contradiction $a^2=F(0)=F(v(0))=F(v(x_0))=0$. In particular, this means that $u(v(x)) < a$ and the rhs of the second equation of (1) is strictly positive.

So, $av(x)\le u(v(x))\le a$ and we have $v(x)\in[0,1]$ for all $x\ge0$. Let us now define $\mathcal{S}$ to be the space of continuous functions $v\colon[0,\infty)\to[0,1]$ with $v(0)=0$. Then, for any $v_0\in\mathcal{S}$ consider constructing functions $u,v\colon[0,\infty)\to\mathbb{R}$ by $u(0)=v(0)=0$ and \begin{align} &u^\prime(x)=a+v_0(x),\\ &v^\prime(x)=(a+v(x))(a-u(v(x))). \end{align} The first of these is solved by an integral, and we have $u(x)\ge ax$. The right hand side of the second equation is then a differentiable function of $v(x)$. So, by the standard Picard–Lindelöf theorem it has a unique solution and, as we showed above, $v^\prime(x) > 0$ for all $x$, so $v\ge0$. So, $u(v(x)) <a$ implying, as above, that $v\in\mathcal{S}$. Hence we can define $\Gamma\colon\mathcal{S}\to\mathcal{S}$ by $\Gamma v_0=v$ where $v_0,v$ are as above. Note that if $(u,v)$ solve (1) then we have $\Gamma v=v$ and, conversely, if $\Gamma v=v$ then $(u,v)$ solves (1), where $u(x)=\int_0^x(a+v(y))dy$. So, existence and uniqueness of solutions to (1) is equivalent to $\Gamma$ having a unique fixed point. The fact that $u,v$ are strictly increasing with $u\to\infty$ follows from $u^\prime > a$, $v^\prime > 0$, which we have shown already.

In practise, the iterates $\Gamma^nv$ of converges very quickly to a fixed point for all values of $a > 0$ which I tried, and this was used to generate the plots of $f$ above.

We will start with the case where $a\in(0,1]$. Then, $v=\Gamma v_0$ satisfies \begin{align} v^\prime&=(a+v)(a-u(v))\le(a+v)(a-av)\\ &=a(a+v)(1-v)\le\frac14a(1+a)^2\le1. \end{align} In particular, $v(x)\le x$, so $\Gamma v_0(x)$ is a function of the path of $v_0$ on the range $[0,x]$. This means that solving the ODE (1) involves computing the derivative $v^\prime(x)$ in terms of the values of $v$ already computed on $[0,x]$, so we can step continuously forwards in time, and the approach is similar to standard ODE solving. We can show the following.

There exists constants $A,B>0$ such that, for any $v_0,\tilde v_0\in\mathcal{S}$, and $v=\Gamma v_0$, $\tilde v=\Gamma\tilde v_0$ then, \begin{align} \lvert v^\prime(x)-\tilde v^\prime(x)\rvert\le A\lvert v(x)-\tilde v(x)\rvert+B\sup_{y\le x}\lvert v_0(y)-\tilde v_0(y)\rvert.&&{\rm(3)} \end{align} Proof: Using the expression for $v^\prime$ and, similarly for $\tilde v^\prime$, \begin{align} v(x)-\tilde v(x) &= (a-\tilde u(\tilde v))(v-\tilde v)+(a+v)(\tilde u(\tilde v)-u(v))\\ &=(a-\tilde u(\tilde v))(v-\tilde v)-(a+v)(\tilde u(v)-\tilde u(\tilde v))+(a+v)(\tilde u(v)-u(v)) \end{align} As $v$ is bounded by 1 and the derivative of $\tilde u$ is $a+\tilde v_0$, which is bounded by $a+1$, the first two terms on the right hand side of this inequality is bounded by the first term on the right of (3) with $A=(a+1)^2$. As $v(x)\le \min(x,1)$, the final term in this inequality is bounded by $$ (a+1)\int_0^v(\tilde v_0(y)-v_0(y))dy\le (a+1)v(x)\sup_{y\le v(x)}\lvert \tilde v_0(y)-v_0(y)\rvert. $$ So, we get (3) with $B=a+1$.

So, if we define $\varphi_0(x)=\sup_{y\le x}\lvert v_0(y)-\tilde v_0(y)\rvert$ and $\varphi(x)=\sup_{y\le x}\lvert v(y)-\tilde v(y)\rvert$, then $$ \varphi^\prime(x)\le A\varphi(x)+B\varphi_0(x). $$ For any $C > A+B$, we can solve this as \begin{align} e^{-Cx}\varphi(x)&\le B\int_0^xe^{-(C-A)(x-y)}e^{-Cy}\varphi_0(y)\,dy\\ &\le\frac{B}{C-A}\left(1-e^{-(C-A)x}\right)\sup_{y\le x}e^{-Cy}\varphi_0(y). \end{align} Hence, using the norm $\Vert v\rVert=\sup_xe^{-Cx}\lvert v(x)\rvert$ on $\mathcal{S}$, $\Gamma$ is Lipschitz continuous with constant $B/(C-A) < 1$. The Banach fixed point theorem implies that $\Gamma$ has a unique fixed point.

For $a > 1$ the ODE (1) has $v^\prime(0) > 1$, so $v(x) > x$ at least for small positive values of $x$. This means that the expression $v^\prime(x)$ involves computing $v(y)$ for values of $y > x$. This means that we cannot solve the ODE by continuously stepping forwards from $x=0$. In such cases, we are not guaranteed that solutions exist or are unique. However, numerically applying $\Gamma$ iteratively to an arbitrarily chosen $v\in\mathcal{S}$ does converge quickly to a fixed point, which I used to compute $f$ in the plots above. In fact, it can be shown that $\Gamma$ is a contraction on $\mathcal{S}$ under the uniform norm.

To complete the proof for $a > 1$, the following shows that $\Gamma$ is a contraction and the Banach fixed point theorem guarantees a unique fixed point. We will work using the supremum norm $\lVert v\rVert=\sup_x\lvert v(x)\rvert$ on $\mathcal{S}$.

For $a\ge1$, $\Gamma$ is Lipschitz continuous on $\mathcal{S}$ with coefficient $a^{-1}$.

It is enough to prove this in an infinitesimal sense. If $v_0,v_1\in\mathcal{S}$ then $v_t=(1-t)v_0+tv_1\in\mathcal{S}$ for $t\in[0,1]$, $\dot v_t=v_1-v_0$ and, $$ \Vert \Gamma v_1-\Gamma v_0\rVert\le\int_0^1\left\lVert\frac{d}{dt}\Gamma v_t\right\rVert\,dt. $$ If we can show that $\lVert (d/dt)\Gamma v_t\rVert\le a^{-1}\lVert\dot v_t\rVert$ then we are done. Setting $\tilde v=\Gamma v_t$, $w=(d/dt)\Gamma v_t$, we can differentiate the definition of $\Gamma v_t$ to obtain, \begin{align} w^\prime &= w(a-u(\tilde v))+(a+\tilde v)(-\dot u(\tilde v)-u^\prime(\tilde v)w),\\ u^\prime(\tilde v)&=a+v_t(\tilde v)\ge a,\\ u(\tilde v) & \ge a\tilde v,\\ \lvert \dot u(\tilde v)\rvert &=\frac{d}{dt}\left\lvert\int_0^\tilde v(a+v_t(y))dy\right\rvert\le\int_0^\tilde v\lvert\dot v_t(y)\rvert\,dy\le\tilde v\lVert \dot v_t\rVert. \end{align} Multiplying the ODE for $w$ by the sign of $w$ and substituting in the inequalities gives $$ \lvert w\rvert^\prime\le\lvert w\rvert a(1-\tilde v)+(a+\tilde v)(\tilde v\lVert v_t\rVert-a\lvert w\rvert). $$ The right hand side is a quadratic in $\tilde v$ with a positive coefficient of $\tilde v^2$, so its maximum over the range $\tilde v\in[0,1]$ is obtained at the endpoints. Therefore, $$ \lvert w\rvert^\prime\le\max\left(-\lvert w\rvert a(a-1),(a+1)(\lVert v_t\rVert-a\lvert w\rvert)\right). $$ So, $\lvert w\rvert^\prime \le 0$ whenever $\lvert w\rvert\ge a^{-1}\lVert v_t\rVert$. It follows that $\lvert w(x)\rvert\le a^{-1}\lVert v_t\rVert$ for all $x$, as required.

Answer 2

There are two solutions:

$$\displaystyle f_1(x) = e^{\frac{\pi}{3} (-1)^{1/6}} x^{\frac{1}{2}+\frac{i \sqrt{3}}{2}}$$

$$\displaystyle f_2(x) = e^{\frac{\pi}{3} (-1)^{11/6}} x^{\frac{1}{2}+\frac{i \sqrt{3}}{2}}$$

See here for details on how to solve such equations.

Answer 3

Given any function $f$ defined in the neighborhood of $c$ and satisfying $f(c)=b\ne c$, $f'(c)\ne0$ we can define $f$ in a neighborhood $V$ of $b$ such that $$f'(x)\equiv f\bigl(f(x)\bigr)\tag{1}$$ in a neighborhood $U$ of $c$: The function $f$ maps a suitable neighborhood $U$ of $c$ bijectively onto a neighborhood $V$ of $b$, and we may assume that $U\cap V=\emptyset$. Now define $$f(y):=f'\bigl(f^{-1}(y)\bigr)\qquad(y\in V)\ ,$$ and $(1)$ is satisfied for all $x\in U$.

It follows that interesting examples come from your approach looking for an $f$ satisfying $(1)$ with $f(c)=c$ for some $c$. For the discussion of such $f$'s we move the fixed point to the origin and cosider the function $$g(t):=f(c+t)-c$$ instead. It follows that $g(0)=0$, and $$g'(t)=f'(c+t)=f\bigl(f(c+t)\bigr)=f\bigl(g(t)+c\bigr)=g\bigl(g(t)\bigr)+c\ .$$ In order to solve $$g'(t)=g\bigl(g(t)\bigr)+c$$ we now make the ''Ansatz'' $$g(t)=c\>t +\sum_{k=2}^\infty a_k t^k$$ and compare coefficents. Mathematica produces $$\eqalign{g(t)=c t &+ {1\over2}c^2 t^2 + {1\over6} (c^3 + c^4) t^3 + {1\over24} (c^4 + 4 c^5 + c^6 + c^7) t^4 \cr &+ {1\over120} (c^5 + 11 c^6 + 11 c^7 + 8 c^8 + 4 c^9 + c^{10} + c^{11}) t^5 \cr&+ {1\over720} (c^6 + 26 c^7 + 66 c^8 + 58 c^9 + 60 c^{10} + 22 c^{11} + 22 c^{12} + 8 c^{13} + 4 c^{14} + c^{15} + c^{16}) t^6 \cr&+{1\over5040}(c^7 + 57 c^8 + 302 c^9 + 424 c^{10} + 553 c^{11} + 387 c^{12} + 319 c^{13} + 220 c^{14} + 122 c^{15} \cr&\qquad\qquad+ 76 c^{16} + 38 c^{17} + 22 c^{18} + 8 c^{19} + 4 c^{20} + c^{21} + c^{22}) t^7\cr &\ +?\ t^8\ .\cr}$$ This is more or less what you did, but now we have $c$ ($=-0.6$ in your example) as a parameter.

Answer 4

The answer to the question, is, with some probability, YES, locally.

I will explain how to transform the equation into another one, and then try to convince you that there should exist a theorem analogous to the fundamental theorem for ODE that solves the problem (I have not the time to prove the theorem, or to seek it in the literature, but I strongly believe it should exist somewhere, in this or other form).

Assume that there is a small interval $[a,b]$ where $f'(x)>0$ or $f'(x)<0$. In particular, if it is demanded that $f'$ be continuous, there should exist such an interval unless there is no other solution but $f=0$.

We suppose w.l.g that $f'(x)>0$, so $f$ is strictly increasing, hence invertible $[a,b]\to [c,d]$. In $[a,b]$, there holds $$f'(x)=f(f(x)),$$ hence in $[c,d]$, there holds $$f'(f^{-1}(x)) = f(x);$$ in particular, $f(x)>0$ in $[c,d]$. The previous equation is equivalent to $${1\over f'(f^{-1}(x))} = {1\over f(x)}$$ (no problem of division by $0$ here). Equivalently, $$(f^{-1})'(x) = {1\over f(x)}.$$ Set $g=f^{-1}$, so $$g'(x) = {1\over g^{-1}(x)}$$.

This equation is of the form $$y' = F(y^{-1}, x)\quad (*),$$ analogous to the ordinary differential equation $y'= F(y,x)$. We would like to solve it using a one step schema, but the problem is that if you know $y$ in some interval, you know $y^{-1}$ in another one (as pointed out by Julien). Nevertheless, if $y$ is assumed to intersect the axis $y=x$ at some point $x^*$, (this is the case here since it has been shown that $f$ has one fixed point), then I believe this problem can be overcome by building "simultaneously" the four branchs intersecting at this point, using a certain schema. At point $x^*$, $y = y^{-1}$, so we know $y'(x^*)$, and we can build (approximately) a small part of the branch of $y$ near $y(x^*)$; then, we can build the symmetric part of this branch around the axis $y=x$, that is, a small part of $y^{-1}$; hopefully, we continue in this way. The schema is probably not so easy because it should be necessary in general to build one branch faster than the second. I leave this interesting problem, namely the solution of an equation of the form $y'(x)=f(y^{-1}(x),x)$ whenever $y(x^*)=y^{-1}(x^*)$ for some $x^*$, to the reflection of the readers (these remarks are only a direction of research, not a demonstration in any way).

Answer 5

Assume that there exists such a function, since $f'(x)=f(f(x))>0$, the function is strictly monotone increasing. By the monotonity, $f(x)>0$ implies $f(f(x)>f(0)$ for all $x$. Thus, $f(0)$ is a lower bound for $f'(x)$ and, for all $x<0$, we have $f(x)<f(0)+xf(0)=(1+x)f(0)$. Hence, if $x\le -1$, then $f(x)\le 0$, contradicting the property $f(x)>0$.

So such function does not exist.

Or you can see this post.

Answer 6

. Suppose that $f' = f(f)$. By the fact that $f(f) = f' > 0$ and $f$ is an injection, either $f > 0$ or $f < 0$. Then for any $a$, $b$ $\in \mathbb{R}$ where $a < b$, by change of variables: $$ b - a = \int^b_a \frac{f'(x)}{f(f(x))} dx = \int^{f(b)}_{f(a)} \frac{1}{f(y)} dy $$ However, we know that since $f(a) < f(b)$ $$ \frac{f(b)-f(a)}{f(b)} \leq \int^{f(b)}_{f(a)} \frac{1}{f(x)} dx \leq \frac{f(b)-f(a)}{f(a)} $$ Thus, we have $$ f(a) \leq \frac{f(b) - f(a)}{b-a} \leq f(b) $$ Thus, $f' = f$. This implies that $f = e^x$. However, since $f(f(x)) = f' = f $, we have that $f = x$. This is a contradiction,

so much function does not exist.