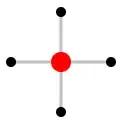
In a graph-theoretic context the following question arose:
Given a natural number $n$. In how many ways can it be written as the sum of composite numbers?
As an example, the number $64$ can be written as $60+4$ , $58+6$ , $56+8$ , $56+4+4$ , $54+10$ , $54+6+4$ , $\dots$ , $32+32$, $32+28+4$,$\dots$
The graph-theoretic background of this question was the following. The vertex-induced subgraph
may appear 64 times in a graph with 64 vertices. There are many random graphs with this property, but some graphs are sets of disjoint torified rectangular square grids. (Torified means that opposite vertices on the sides of a rectangular square grid are connected.) For example two torified square grids with 4x8 vertices each, or four torified square grids with 2x4 vertices each. So the number of such multiple torus graphs is the number I am looking for (for $64$).
In other words: I am looking for the composite partition function of natural numbers.
Thanks to player3236's hint now I know the answer for $64$: it is $2357$. But it would be great to know the number of all graphs with the above property. I assume this will be a really big number, but it might be impressive to see exactly how small the fraction of regular graphs with this property is, and that it will tend to 0 for really large graphs. Is there a way to estimate it? But I admit, this is another question.