Graph puzzles: Constructing graphs from tiles

Question

There is a vast literature on the reconstruction conjecture which says that two graphs with the same deck $D$ are isomorphic. The deck is the multi-set of vertex-deleted subgraphs of a graph (which are called cards).

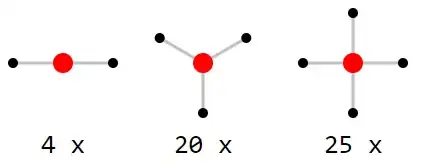
I'd like to take the other perspective and start with the multi-set $T$ of so-called tiles of a graph which are the vertex-induced subgraphs of the graph containing a distinguished vertex, all of its neighbours, and all the edges between them. As for $D$, $T$ contains as many elements as there are nodes in the graph: one tile for each.

Different from $D$, the tile set $T$ of a graph can be the tile set of many other non-isomorphic graphs. Needless to say that for a given multi-set $T$ of possible tiles there may be no graph at all which it is the tile set of.

In case there are many graphs with the same tile set $T$, these may share or may share not a lot of graph properties like being connected or having a small diameter. The only property theses graphs do share for sure is the degree distribution which is immediately given by the tile set.

Some tile sets may define a unique graph. I assume this is the case for this one, but I may be wrong:

Puzzle 1

Can you find a solution to this puzzle? Solving the puzzle means to put together tiles by identifying nodes or edges while the red dots must not match black ones. Note, that the Euclidean lengths of edges in the final graph doesn't have to match the lengths of edges in the tiles when embedding them in some Euclidean space: you can stretch them however you want. (By the way, this is not necessary in these examples.)

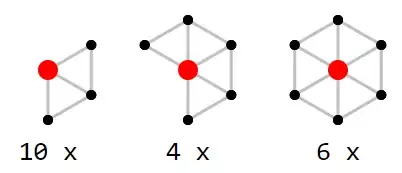
Try out this one:

Puzzle 2

My questions are:

1. If $T$ is guaranteed to be the tile set of a graph which you don't know (like in the examples above): by which algorithm would you construct any graph which $T$ is the tile set of?
   _{While this algorithm is probably some kind of a search algorithm, I added the [searching] tag.}

2. How to prove that for any given set $T$ of tiles

   1. there is no graph with tile set $T$

   2. there are exactly $n$ graphs with tile set $T$ (for small $n$)

   3. there are really many graphs with tile set $T$ (e.g. $\mathcal{O}(|T|^\alpha)$)

   4. there is a graph with tile set $T$, but only with a small fraction $\epsilon$ of tiles left.

In case there are really many graphs with the same tile set $T$, these may be considered as a family of random graphs (= all graphs with tile set $T$). What may be said about this family of random graphs? Note, that in case you have an algorithm that generates a solution (question 1) you will have to randomize it to generate other random graphs with tile set $T$.

Since these questions seem so natural, I would imagine that they have been asked before. In this (probable) case, I would be happy to get a reference where I will find them answered. And a search term I can scholar-google for.

---

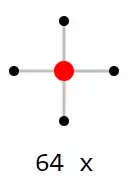
For those who like to puzzle and find out from which (non-random) graphs some given tile sets originated, here are two more puzzles. (Spoiler alert: Solutions are given in an answer below.)

Puzzle 3

Puzzle 4

Answer 1

As a partial answer, here is how we can solve the sampling problem in cases like your first tile set: triangle-free tile sets. When lots of triangles get involved, the problem becomes much harder.

A random graph with the degree sequence $$(2, 2, \underbrace{3, 3, \dots, 3}_{20}, \underbrace{4,4,\dots,4}_{25})$$ can be generated by sampling from the configuration model. Generally, this will produce multigraphs with loops and parallel edges, but we're unlikely to get many of these, and repeated sampling will typically give us a simple graph after only a few trials.

In a similar way, repeated sampling will typically give us a graph with no $3$-cycles after only a few trials: short cycles are unlikely in sparse graphs with a given degree sequence. If a graph with no $3$-cycles has the degree sequence above, its tile set should be exactly the one you gave.

In practice, the Mathematica code

RandomGraph[DegreeGraphDistribution[{2, 2}~Join~Table[3, 20]~Join~Table[4, 25]]]

produces a graph with no $3$-cycles pretty efficiently (over $100$ experiments, the average number of trials required was $19.94$). By the way, all $100$ graphs I generated were different, so the solution is far from unique.

Answer 2

Solution to Puzzle 3: These are the vertex-induced subgraphs of a 5x5x5 cubic grid.

Solution to Puzzle 4: These are the vertex-induced subgraphs of a torified 8x8 square grid.